[mathjax]
目次
1/30公式
\(\displaystyle\int_{\alpha}^{\beta} (x-\alpha)^2 (x-\beta)^2dx=\displaystyle\frac{1}{30}(\beta-\alpha)^5\)
証明
\(\displaystyle\int_{\alpha}^{\beta} (x-\alpha)^2(x-\beta)^2 dx\)
\(=\biggl[\displaystyle\frac{1}{3}(x-\alpha)^3(x-\beta)^2\biggr]_{\alpha}^{\beta}-\displaystyle\int_{\alpha}^{\beta} \displaystyle\frac{1}{3}(x-\alpha)^3 \cdot 2(x-\beta)dx\) 部分積分
\(=-\displaystyle\frac{2}{3}\biggl(\biggl[\displaystyle\frac{1}{4}(x-\alpha)^4(x-\beta)\biggr]_{\alpha}^{\beta}-\displaystyle\int_{\alpha}^{\beta}\displaystyle\frac{1}{4}(x-\alpha)^4 dx\biggr)\)
\(=\displaystyle\frac{1}{6}\biggl[\displaystyle\frac{1}{5}(x-\alpha)^5 \biggr]_{\alpha}^{\beta}\)
\(=\displaystyle\frac{1}{30}(\beta-\alpha)^5\)
一般化
一般化した公式は以下の記事のぜひ。

面積計算
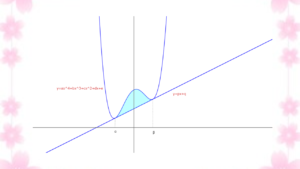
\(\displaystyle\frac{1}{30}\)公式を使って、斜線部の面積(\(=S\))を求める。
\(S=\displaystyle\int_{\alpha}^{\beta} \biggl[(px+q)-(ax^4+bx^3+cx^2+dx+e)\biggr]dx\) 面積
\(=\displaystyle\int_{\alpha}^{\beta} -a(x-\alpha)^2 (x-\beta)^2 dx\) 因数分解
\(=-a\cdot\biggl[-\displaystyle\frac{1}{30}(\beta-\alpha)^5 \biggr]\) ※\(\displaystyle\frac{1}{30}\)公式
\(=\displaystyle\frac{a}{30}(\beta-\alpha)^5\)
\(a<0\)の時も考えると面積は \(S=\displaystyle\frac{|a|}{30}(\beta-\alpha)^4\)
こちらを\(\displaystyle\frac{1}{30}\)公式ということも多い。
