[mathjax]
目次
アステロイド
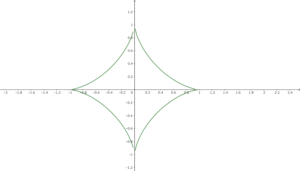
アステロイドとは \(x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}\) で表される図形のことで、星芒形とも呼ばれる。
アステロイドの媒介変数表示
\(x=a\cos^3 \theta\)
\(y=a\sin^3 \theta\)
媒介変数表示や図形が\(x\)軸\(y\)軸に関して対称であることを利用して面積と長さと体積を計算していく。
計算
面積
対称性を利用。図形は\(x\)軸\(y\)軸に関して対称なので第一象限の面積の4倍と考える。
\(S=4\displaystyle\int_{0}^{a} y dx\)
\(=4\displaystyle\int_{\frac{\pi}{2}}^{0} (a\sin^3\theta)(-3a\cos^2\theta\sin\theta) d\theta\)
\(=12a^2\displaystyle\int_{0}^{\frac{\pi}{2}} \sin^4\theta\cos^2\theta d\theta\)
\(=12a^2\displaystyle\int_{0}^{\frac{\pi}{2}} \sin^4\theta(1-\sin^2\theta) d\theta\)
\(=12a^2\biggl[\displaystyle\int_{0}^{\frac{\pi}{2}} \sin^4\theta d\theta-\displaystyle\int_{0}^{\frac{\pi}{2}} \sin^6\theta d\theta\biggr]\)
https://kikyousan.com/mathbottop/integralbot/integralbot40
の結果を使うと
\(=12a^2\biggl(\displaystyle\frac{3!!}{4!!}\cdot\displaystyle\frac{\pi}{2}-\displaystyle\frac{5!!}{6!!}\cdot\displaystyle\frac{\pi}{2}\biggr)\)
\(=\displaystyle\frac{3}{8}\pi a^3\)
曲線の長さ
これも対称性を利用する。
\(l=4\displaystyle\int_{0}^{\frac{\pi}{2}} \sqrt{\biggl(\displaystyle\frac{dx}{d\theta}\biggr)^2+\biggl(\displaystyle\frac{dy}{d\theta}\biggr)^2} d\theta\)
\(=4\displaystyle\int_{0}^{\frac{\pi}{2}}\sqrt{(-3a\cos^2\theta\sin\theta)^2+(3a\sin^2\theta\cos\theta)^2}d\theta\)
\(=4\displaystyle\int_{0}^{\frac{\pi}{2}}\sqrt{9a^2\cos^2\theta\sin^2\theta(\cos^2\theta+\sin^2\theta)}d\theta\)
\(=4\displaystyle\int_{0}^{\frac{\pi}{2}}3a|\cos\theta\sin\theta|d\theta\)
\(=6a\displaystyle\int_{0}^{\frac{\pi}{2}}|\sin 2\theta|d\theta\)
\(0\leq \theta\leq\displaystyle\frac{\pi}{2}\)では \(\sin 2\theta\geq 0\)より絶対値を外せる。
\(=6a\displaystyle\int_{0}^{\frac{\pi}{2}}\sin 2\theta d\theta\)
\(=6a\biggl[-\displaystyle\frac{1}{2}\cos 2\theta\biggr]_{0}^{\frac{\pi}{2}}\)
\(=6a\)
体積
アステロイドを\(x\)軸まわりに回した時の回転体の体積を求める。(軸はどちらでもよいが)
\(V=2\displaystyle\int_{0}^{a} \pi y^2 dx\)
\(=2\displaystyle\int_{\frac{\pi}{2}}^{0} \pi a^2\sin^6\theta (-3a\cos^2\theta\sin\theta)d\theta\)
\(=6\pi a^3 \displaystyle\int_{0}^{\frac{\pi}{2}} (\sin^7\theta-\sin^9\theta)d\theta\)
https://kikyousan.com/mathbottop/integralbot/integralbot40 の結果を使うと
\(=6\pi a^3\biggl(\displaystyle\frac{6\cdot 4\cdot 2}{7\cdot 5\cdot 3\cdot 1}-\displaystyle\frac{8\cdot 6\cdot 4\cdot 2}{9\cdot 7\cdot 5\cdot 3\cdot 1}\biggr)\)
\(=\displaystyle\frac{32}{105}\pi a^3\)
接線
アステロイド上の点(軸上は除く)における接線が座標軸によって切り取られる距離は一定になるという面白い性質があります。これを証明します。
アステロイド上の点\((a\cos^3\theta,a\sin^3 \theta)\)での接線は
傾きが
\(\displaystyle\frac{dy}{dx}=\displaystyle\frac{\displaystyle\frac{dy}{d\theta}}{\displaystyle\frac{dx}{d\theta}}=\displaystyle\frac{3a\sin^2\theta}{-3a\cos^2\theta\sin\theta}\)
\(=-\tan\theta\)
であるので接線は
\(y=-\tan\theta(x-a\cos^3\theta)+a\sin^3\theta\)
\(=-(\tan\theta)x+a\sin\theta(\sin^2\theta+\cos^2\theta)\)
\(=-(\tan\theta)x+a\sin\theta\)
\(x\)切片(\(y=0\))は\((-a\cos\theta,0)\)
\(y\)切片(\(x=0\))は\((0,a\sin\theta)\)
なので、切り取る距離の長さは
\(\sqrt{(-a\cos\theta)^2+(a\sin\theta)^2}=a\)
となり、一定値を取る。

