[mathjax]
目次
サイクロイドとは
\(x=a(\theta-\sin\theta)\)
\(y=a(1-\cos\theta)\)
(\(0\leq\theta<2\pi\)) の媒介変数表示で表される曲線。
ちなみにサイクロイドは、円が転がる時に定点が描く曲線です。
最速降下曲線もサイクロイドです。
では、サイクロイドの曲線の長さと面積を求めていきます。
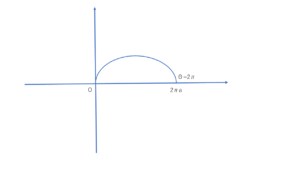
面積
\(\displaystyle\int_{0}^{2\pi a}y dx\) ※\(\theta=2\pi\) のとき \(x=2\pi a\)
\(=\displaystyle\int_{0}^{2\pi} a(1-\cos\theta)\cdot a(1-\cos\theta) d\theta\) \(\displaystyle\frac{dx}{d\theta}=a(1-\cos\theta)\)
\(=a^2\displaystyle\int_{0}^{2\pi} (1-2\cos\theta+\cos^2\theta)d\theta\)
\(=a^2\displaystyle\int_{0}^{2\pi} \biggl(1-2\cos\theta+\displaystyle\frac{1+\cos 2\theta}{2}\biggr)d\theta\) ※半角公式
\(=a^2\biggl[\theta-2\sin\theta+\displaystyle\frac{1}{2}\theta+\displaystyle\frac{1}{4}\sin 2\theta\biggr]_{0}^{2\pi}\)
\(=3\pi a^2\)
曲線の長さ
\(L=\displaystyle\int_{0}^{2\pi} \sqrt{\biggl(\displaystyle\frac{dx}{d\theta}\biggr)^2+\biggl(\displaystyle\frac{dy}{d\theta}\biggr)^2}d\theta\)
\(=\displaystyle\int_{0}^{2\pi} \sqrt{a^2(1-\cos\theta)^2+a^2\sin^2 \theta} d\theta\)
\(=a\displaystyle\int_{0}^{2\pi} \sqrt{2-2\cos\theta} d\theta\) ※整理した
\(=a\displaystyle\int_{0}^{2\pi}\sqrt{4\sin^2 \displaystyle\frac{\theta}{2}} d\theta\) ※半角公式利用 \(\displaystyle\frac{1-\cos\theta}{2}=\sin^2\displaystyle\frac{\theta}{2}\)
\(=a\displaystyle\int_{0}^{2\pi} 2 \sin\displaystyle\frac{\theta}{2} d\theta\) ※\(0\leq \theta<2\pi\) で \(\sin\displaystyle\frac{\theta}{2}\geq 0\)より絶対値は外せる。
\(=4a\biggl[-\cos\displaystyle\frac{\theta}{2}\biggr]_{0}^{2\pi}\)
\(=8a\)

