目次
斜軸回転の体積
回転体の体積で、斜めの軸まわりの場合を考えます。
問題
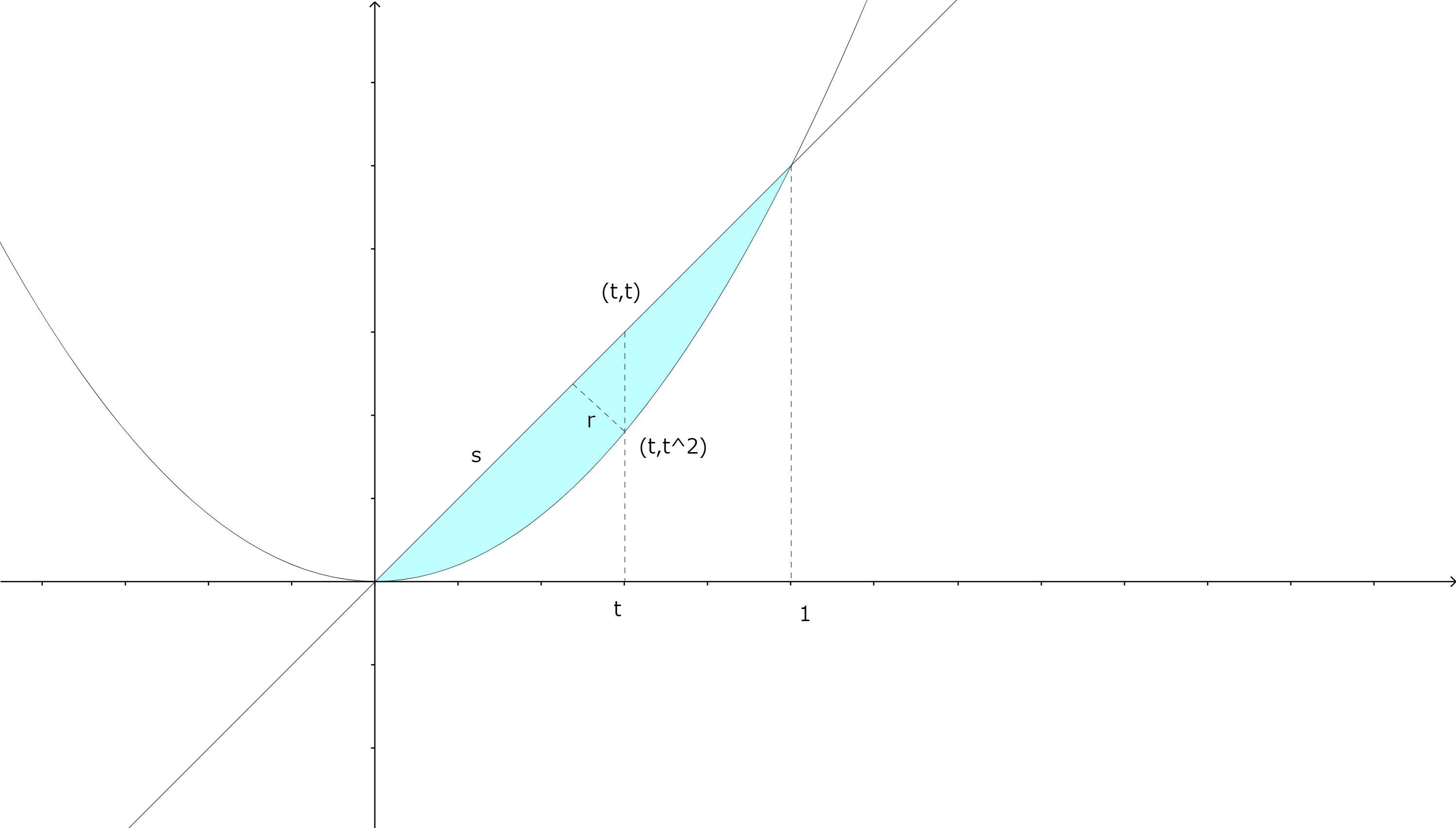
\(y=x^2\)と\(y=x\)で囲まれる部分を\(y=x\)軸まわりに回転させてできる立体の体積は?
解答
\(r=\displaystyle\frac{t-t^2}{\sqrt{2}}\)。および \(\sqrt{2} t=s+r\)より \(s=\displaystyle\frac{t+t^2}{\sqrt{2}}\)
\(V=\displaystyle\int_{0}^{\sqrt{2}} \pi r^2 ds\)
※\(y=x\)を軸とみた場合の通常通りの体積計算。
\(=\displaystyle\int_{0}^{1} \pi \biggl(\displaystyle\frac{t-t^2}{\sqrt{2}}\biggr)^2 \times \displaystyle\frac{1+2t}{\sqrt{2}} dt\)
※枠内の関係式を使って変形した。
\(=\displaystyle\frac{\pi}{2\sqrt{2}} \displaystyle\int_{0}^{1} (2t^5-3t^4+t^2)dt\)
\(=\displaystyle\frac{\pi}{2\sqrt{2}}\biggl[\displaystyle\frac{1}{3}t^6-\displaystyle\frac{3}{5}t^5+\displaystyle\frac{1}{3}t^3\biggr]_{0}^{1}\)
\(=\displaystyle\frac{\sqrt{2}}{60}\pi\)
裏技公式(傘型分割)
計算するだけの場合におすすめです。
\(y=ax\)と\(y=f(x)\)で囲まれる領域を\(y=ax\)まわりでまわしてできる体積は
\(V=\pi\cos\theta\displaystyle\int_{\alpha}^{\beta} (ax-f(x))^2 dx\)
※\(\theta\)は\(y=ax\)と\(x\)軸のなす角。
\(\alpha\)、\(\beta\)は交点で\(\alpha<\beta\)
体積を傘のように分割して(円錐の表面積)足しあげている。
円錐の表面積は「\(\pi\times (母線の長さ)\times (底面の半径)\)」でこれを当てはめると
\(\pi\times(ax-f(x))\times((ax-f(x))\cos\theta)\)
これを足し上げるので上の公式のようになる。(※あくまでイメージ)
実際に先ほどの例題で計算をして見ましょう。
\(V=\pi\cos\theta\displaystyle\int_{\alpha}^{\beta} (ax-f(x))^2 dx\)
\(=\displaystyle\frac{\pi}{\sqrt{2}} \displaystyle\int_{0}^{1} (x-x^2)^2 dx\)
\(=\displaystyle\frac{\pi}{\sqrt{2}} \biggl[\displaystyle\frac{1}{5}x^5-\displaystyle\frac{1}{2}x^4+\displaystyle\frac{1}{3}x^3\biggr]_{0}^{1}\)
\(=\displaystyle\frac{\sqrt{2}\pi}{60}\)