目次
問題

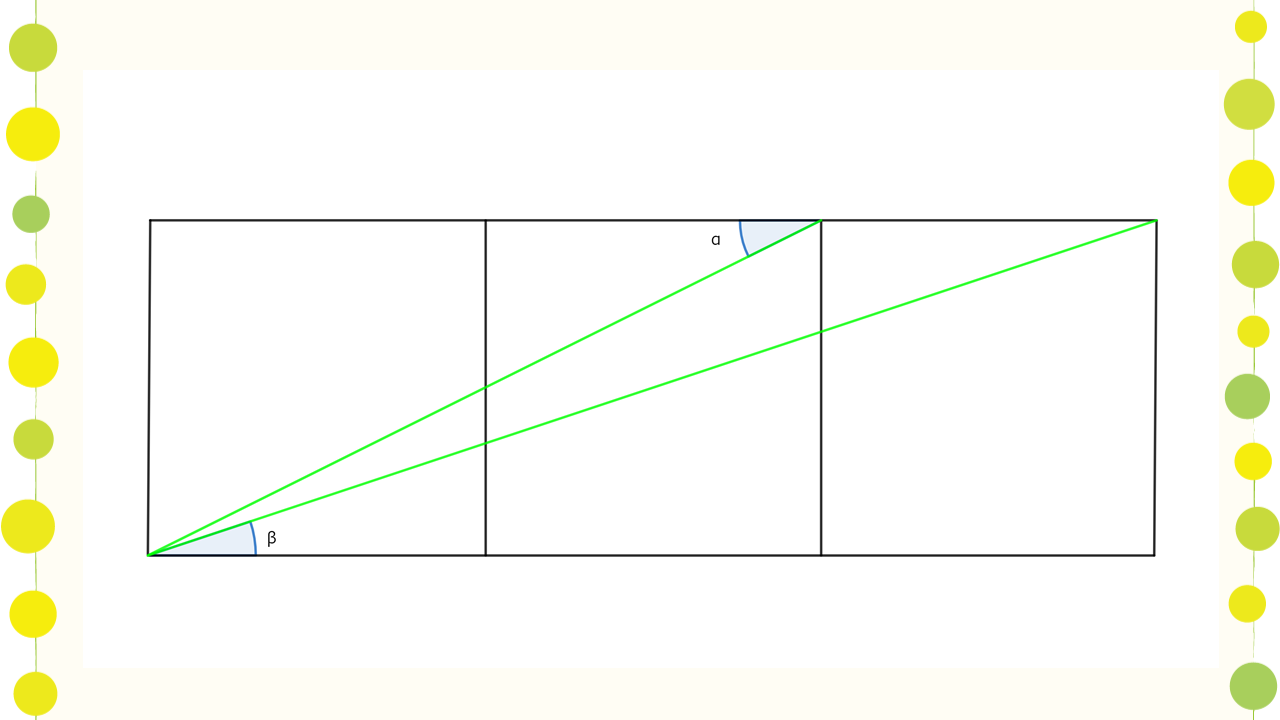
3つの正方形を並べ、角を上のようにとる。
この時、上図において\(\alpha+\beta=\displaystyle\frac{\pi}{4}\) (=45°) が成立。
証明1 三角関数
図より \(\tan \alpha=\displaystyle\frac{1}{2}\) \(\tan \beta=\displaystyle\frac{1}{3}\) であり、加法定理を使って以下のものを計算する。
\(\tan (\alpha+\beta)=\displaystyle\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}=\displaystyle\frac{\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}}{1-\displaystyle\frac{1}{2}\times\displaystyle\frac{1}{3}}=1\)
\(0<\alpha,\beta< \displaystyle\frac{\pi}{2}\)より \(0 < \alpha+\beta < \pi\)
\(\alpha+\beta=\displaystyle\frac{\pi}{4}=45^{\circ}\)となる。
証明2 幾何
まず、下の図のように問題の図を折り返す。
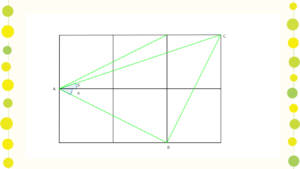
三角形ABCを考える。比が重要で絶対的な長さに意味はないので、正方形の一辺の長さを1とする。
$$AB=\sqrt 5,BC=\sqrt 5,CA=\sqrt 10$$
よって三角形ABCは角B=90°の直角二等辺三角形。
\(\alpha+\beta=\displaystyle\frac{\pi}{4}\)
証明3 複素数
3つの正方形の左下を原点として長さ1で座標設定。
\(\gamma=2+i\) 、\(\delta=3+i\) とおく。 \(\arg \gamma=\alpha\) 、\(\arg \delta=\beta\) となる。
ここで \(\gamma\delta=5+5i=5\sqrt 2(\cos \displaystyle\frac{\pi}{4}+i\sin \displaystyle\frac{\pi}{4}) \)
よって \(\alpha+\beta=\arg \gamma+\arg \delta=\arg \gamma\delta=\displaystyle\frac{\pi}{4}=45^{\circ}\)