[mathjax]
目次
サイクロイド 最速降下線
球を転がすときに、最もはやく転がる時の軌跡はサイクロイドになる。
計算
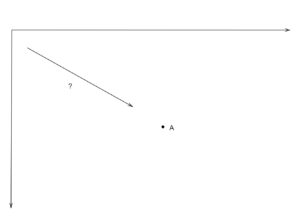
上のような状況を考える。(矢印は直線で書かれてますが、最終的な結果はサイクロイドです!)
原点から点Aまで最速で下りる経路を変分法を用いて求めます。(重力のみで加速している)
点Aの座標を$(a,b)$とする。
\(T=\displaystyle\int_{0}^{A} \displaystyle\frac{ds}{v}=\displaystyle\int_{0}^{a} \sqrt{\displaystyle\frac{(dx)^2+(dy)^2}{2gy}}\)
\(=\displaystyle\frac{1}{\sqrt{2g}}\displaystyle\int_{0}^{a} \displaystyle\frac{\sqrt{1+\biggl(\displaystyle\frac{dy}{dx}\biggr)^2}}{\sqrt{y}}dx=\displaystyle\frac{1}{\sqrt{2g}}\displaystyle\int_{0}^{a} \sqrt{\displaystyle\frac{1+{y^{\prime}}^2}{y}} dx\)
※エネルギー保存則より、$\displaystyle\frac{1}{2}mv^2=mgy$を解いて$v=\sqrt{2gy}$が導出できる。
$f(y,y^{\prime})=\sqrt{\displaystyle\frac{1+{y^{\prime}}^2}{y}}$としてオイラーラグランジュ方程式を解く。今回、$f$が$x$に依存しないのでこれを利用する。
$\displaystyle\frac{df}{dx}=\displaystyle\frac{\partial f}{\partial x}+\displaystyle\frac{\partial f}{\partial y}\displaystyle\frac{\partial y}{\partial x}+\displaystyle\frac{\partial f}{\partial y^{\prime}}\displaystyle\frac{\partial y^{\prime}}{\partial x}$
$=\displaystyle\frac{d}{dx}\displaystyle\frac{\partial f}{\partial y^{\prime}}y^{\prime}+\displaystyle\frac{\partial f}{\partial y^{\prime}}y^{\prime\prime}=\displaystyle\frac{d}{dx}\left(\displaystyle\frac{\partial f}{\partial y^{\prime}}y^{\prime}\right)$
すなわち、$f-\displaystyle\frac{\partial f}{\partial y^{\prime}}y^{\prime}=C(定数)$と書ける。
今回の$f$を代入すると、$C^2 y(1+{y^{\prime}}^2)=1$となる。
後の計算のため、$\displaystyle\frac{1}{C^2}=2B$と置き換えて$y^{\prime}$について解くと
\(y^{\prime}=\sqrt{\displaystyle\frac{2B}{y}-1}\) ……①
この微分方程式を解く。多少天下り的ではあるが、\(y=B(1-\cos\theta)\) とおく。すると
$dy=B\sin\theta d\theta=2B\sin\displaystyle\frac{\theta}{2}\cos\displaystyle\frac{\theta}{2}d\theta$ (置いた式を微分した)
$y^{\prime}=\sqrt{\displaystyle\frac{1+\cos\theta}{1-\cos\theta}}=\sqrt{\displaystyle\frac{2\cos^2\frac{\theta}{2}}{2\sin^2 \frac{\theta}{2}}}=\displaystyle\frac{\cos\frac{\theta}{2}}{\sin\frac{\theta}{2}}$ (①を変形)
二式から$dy$を消すと、$dx=2B\sin\displaystyle\frac{\theta}{2}d\theta=B(1-\cos\theta)d\theta$
よって、$x=B(\theta-\sin\theta)$ ※初期条件より積分定数は$0$
また、仮定した式より$y=B(1-\cos\theta)$
結果
$x=B(\theta-\sin\theta)$
$y=B(1-\cos\theta)$
これはサイクロイドです。
例 重力トンネル
東京大阪間をサイクロイド形のトンネルを掘って重力によって移動するとする。空気抵抗もろもろを無視すると、先ほどの結果から所要時間は
$T=\displaystyle\frac{1}{\sqrt{2g}}\displaystyle\int_{0}^{a} \sqrt{\displaystyle\frac{1+{y^{\prime}}^2}{y}} dx$
$=\displaystyle\frac{1}{\sqrt{2g}}\displaystyle\int_{0}^{2\pi} \sqrt{\displaystyle\frac{1+\left(\displaystyle\frac{\sin\theta}{1-\cos\theta}\right)^2}{B(1-\cos\theta)}} \displaystyle\frac{dx}{d\theta}d\theta$
$=\displaystyle\frac{1}{\sqrt{2g}}\displaystyle\int_{0}^{2\pi} \sqrt{\displaystyle\frac{2}{B(1-\cos\theta)^2}} B(1-\cos\theta)d\theta$
$=\sqrt{\displaystyle\frac{B}{g}}\displaystyle\int_{0}^{2\pi}d\theta$$=2\pi\sqrt{\displaystyle\frac{B}{g}}$
※$y^{\prime}=\displaystyle\frac{dy}{dx}=\displaystyle\frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}=\displaystyle\frac{\sin\theta}{1-\cos\theta}$
$\theta=2\pi$のとき、$x=2\pi B$であり、$t=\sqrt{\displaystyle\frac{2\pi x}{g}}$で計算できる。
東京大阪間を$500km$とすると、$t\simeq\sqrt{\displaystyle\frac{2\times 3.1415\times 500000}{9.8}}\simeq 566(s)$
なのでおおよそ9分半で到着できる。実際には重力が変化したり空気抵抗があるので実現はできないんですけれどもね笑