目次
電気双極子モーメント 電位と電場
設定
\(+q\)の電荷と\(-q\)の電荷が距離\(l\)だけ(無限小)離れてペアで存在している場合を考える。
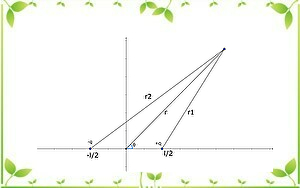
点\(\biggl(\displaystyle\frac{l}{2},0\biggr)\)に電荷\(+q\)、考える点までの距離\(r_{1}\)
点\(\biggl(-\displaystyle\frac{l}{2},0\biggr)\)に電荷\(-q\)、考える点までの距離\(r_{2}\)
中心から考える点までの距離\(r\)とおく。
用語解説
電気双極子 \(\cdots\) 大きさの等しい正負の電荷が無限小間隔で対となっている状態
電気双極子モーメント \(\cdots\) \(\boldsymbol{p}=q\boldsymbol{l}\) のことを指す。(\(-q\)から\(+q\)へのベクトルが\(\boldsymbol{l}\))
電位
\(U=\displaystyle\frac{1}{4\pi\varepsilon_{0}} \cdot\displaystyle\frac{q}{r_{1}}-\displaystyle\frac{1}{4\pi\varepsilon_{0}} \cdot\displaystyle\frac{q}{r_{2}}\)
\(=\displaystyle\frac{q}{4\pi\varepsilon_{0}} \biggl(\displaystyle\frac{1}{\sqrt{r^2+(\frac{l}{2})^2-rl\cos\theta}}-\displaystyle\frac{1}{\sqrt{r^2+(\frac{l}{2})^2+rl\cos\theta}}\biggr)\)
\(=\displaystyle\frac{q}{4\pi\varepsilon_{0}r}\biggl[\biggl(1+\displaystyle\frac{l^2}{4r^2}-\displaystyle\frac{l}{r}\cos\theta\biggr)^{-\frac{1}{2}}-\biggl(1+\displaystyle\frac{l^2}{4r^2}+\displaystyle\frac{l}{r}\cos\theta\biggr)^{-\frac{1}{2}}\biggr]\)
\(\simeq \displaystyle\frac{q}{4\pi\varepsilon_{0}r}\biggl[1-\displaystyle\frac{1}{2}\biggl(\displaystyle\frac{l^2}{4r^2}-\displaystyle\frac{l}{r}\cos\theta\biggr)-1+\displaystyle\frac{1}{2}\biggl(\displaystyle\frac{l^2}{4r^2}+\displaystyle\frac{l}{r}\cos\theta\biggr)\biggr]\)
※双極子間の距離は小さく、観測者からは微小とみなせるので\(l \ll r\)として近似している。
その後に\((1+x)^p\simeq 1+px\) の近似公式を用いている。
\(U=\displaystyle\frac{ql\cos\theta}{4\pi\varepsilon_{0}r^2}\)\(=\displaystyle\frac{\boldsymbol{p}\cdot \boldsymbol{r}}{4\pi\varepsilon_{0}r^3}\)
※\(|p|=ql\)より、\(\boldsymbol{p}\cdot \boldsymbol{r}=qlr\cos\theta\)
電場
$\boldsymbol{E}=-\nabla\phi=-\displaystyle\frac{1}{4\pi\varepsilon_{0}}\left[\displaystyle\frac{1}{r^3}\nabla(\boldsymbol{p}\cdot\boldsymbol{r})+(\boldsymbol{p}\cdot\boldsymbol{r})\nabla\displaystyle\frac{1}{r^3}\right]$$=-\displaystyle\frac{1}{4\pi\epsilon_{0}}\biggl(\displaystyle\frac{\boldsymbol{p}}{r^3}-\displaystyle\frac{3\boldsymbol{r}(\boldsymbol{p}\cdot\boldsymbol{r})}{r^5}\biggr)$
※慣れていなければ成分ごとに計算すれば出てきます。まず、\(x\)成分を求める。
\(E_{x}=-\displaystyle\frac{\partial U}{\partial x}=-\displaystyle\frac{\partial}{\partial x} \biggl[\displaystyle\frac{1}{4\pi\epsilon_{0}}\cdot \displaystyle\frac{p_{x}x+p_{y}y+p_{z}z}{(x^2+y^2+z^2)^{\frac{3}{2}}}\biggr]\)
\(=-\displaystyle\frac{1}{4\pi\epsilon_{0}}\biggl(\displaystyle\frac{p_{x}}{(x^2+y^2+z^2)^{\frac{3}{2}}}-\displaystyle\frac{3x(p_{x}x+p_{y}y+p_{z}z)}{(x^2+y^2+z^2)^{\frac{5}{2}}}\biggr)\)
\(=-\displaystyle\frac{1}{4\pi\epsilon_{0}}\biggl(\displaystyle\frac{p_{x}}{r^3}-\displaystyle\frac{3x(\boldsymbol{p}\cdot\boldsymbol{r})}{r^5}\biggr)\)
\(y\)成分と\(z\)成分も同様にできて結果は \(\boldsymbol{E(\boldsymbol{r})}=-\displaystyle\frac{1}{4\pi\epsilon_{0}}\biggl(\displaystyle\frac{\boldsymbol{p}}{r^3}-\displaystyle\frac{3\boldsymbol{r}(\boldsymbol{p}\cdot\boldsymbol{r})}{r^5}\biggr)\)