抵抗がある場合の斜方投射

[mathjax]

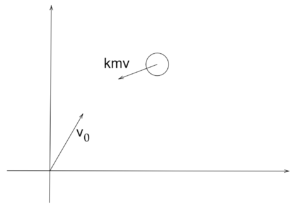
空気抵抗がある場合の斜方投射の運動を計算する。抵抗を速度と質量に比例するとして

$\boldsymbol{F}_{抵抗}=-km\boldsymbol{v}$とおく。

$x,y$それぞれの方向の運動方程式は

$m\dot{v_{x}}=-kmv_{x}$

$m\dot{v_{y}}=-mg-kmv_{y}$

今回の初期条件は、$x_{0}=y_{0}=0$、$v_{x}=v_{0}\cos\theta$、$v_{y}=v_{0}\sin\theta$と考えて微分方程式を解くと

$v_{x}=v_{0}\cos\theta e^{-kt}$

$v_{y}=-\displaystyle\frac{g}{k}+\left(v_{0}\sin\theta+\displaystyle\frac{g}{k}\right)e^{-kt}$

初期条件を考慮して積分すると

$x=\displaystyle\frac{v_{0}}{k}\cos\theta(1-e^{-kt})$

$y=-\displaystyle\frac{g}{k}t+\displaystyle\frac{1}{k}\left(v_{0}\sin\theta+\displaystyle\frac{g}{k}\right)(1-e^{-kt})$

ここから$t$を消去して放物線の方程式を求めたい。$x$方向の式から

$t=-\displaystyle\frac{1}{k}\left(1-\displaystyle\frac{kx}{v_{0}\cos\theta}\right)$

と求まる。また、代入において、以下の対数の展開式を利用する。

$\log(1+x)=x-\displaystyle\frac{x^2}{2}+\displaystyle\frac{x^3}{3}+\cdots$

$y=x\tan\theta-\displaystyle\frac{g}{v_{0}^2\cos^2\theta}\left(\displaystyle\frac{x^2}{2}+\displaystyle\frac{kx^3}{3v_{0}\cos\theta}+\cdots\right)$

第二項まで取り出すと空気抵抗のない場合の放物線と一致する。