[mathjax]
ジェットコースター、よく一回転するものありますよね。
あれが、位置エネルギーだけで回転するためにはどうあればよい??ということを今回計算していきます。
力学での定番問題です。摩擦等は今回なしでの計算になります。
\(h\) …… スタートの高さ
\(m\) ……ジェットコースターの質量
\(g\) ……重力加速度
\(r\) ……一回転するときの半径
目次
計算
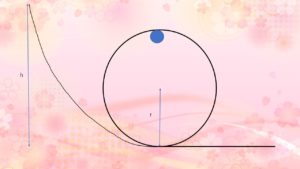
保存則
最高点での速さを\(v\)として「最初」と「最高点」でエネルギー保存則を立てる。
最初は\(mgh\)(位置エネルギーのみ)
最高点は\(\displaystyle\frac{1}{2}mv^2+2mgr\) (運動、位置エネルギー両方ある)
力学エネルギーは保存するので、等号で書くと
\(mgh=\displaystyle\frac{1}{2}mv^2+2mgr\)
これを変形すると \(2mgh-4mgr=mv^2\)
\(m\)で割ると \(v^2=2gh-4gr\)
一回転
一回転する=最高点で落ちない=最高点で垂直抗力が存在
\(N=\displaystyle\frac{mv^2}{r}-mg \geq 0\) であるとき一回転する。(\(N\)は垂直抗力)
ここで、\(v^2\)の所に保存則で出した式を代入。
\(\displaystyle\frac{2mgh-4mgr}{r}-mg\geq 0\)
\(\displaystyle\frac{2mgh}{r}-5mg\geq 0\)
\(h\geq \displaystyle\frac{5}{2}r\)
となる。つまり、円半径の2.5倍の高さから落下すれば一回転する。
半径が\(20(m)\) だとすると、\(50(m)\) 以上の高さから落下していないといけない。

