目次
ドーナツの体積
ドーナツの形の体積を求めます。円を軸まわりにぐるっと回転させたと考えます。トーラスの一種。
設定
\(0\leq a\leq b\)とする。以下の図形を\(x\)軸まわりに回転させたものと考えて計算する。
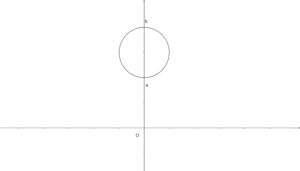
計算
「断面で円の上側を回した時にできる立体」\(-\)「断面で円の下側を回した時にできる立体(空洞部分)」で計算します。円の方程式は
\(x^2+\biggl(y-\displaystyle\frac{a+b}{2}\biggr)^2=\biggl(\displaystyle\frac{b-a}{2}\biggr)^2\)
\(y\)について解くと \(y=\displaystyle\frac{a+b}{2}\pm \sqrt{\biggl(\displaystyle\frac{b-a}{2}\biggr)^2-x^2}\)
よって体積は
\(V=\displaystyle\int_{-\frac{b-a}{2}}^{\frac{b-a}{2}} \pi(y_{上}^2-y_{下}^2)dx\)
\(=2\pi\displaystyle\int_{0}^{\frac{b-a}{2}} \biggl[\biggl(\displaystyle\frac{a+b}{2}+ \sqrt{\biggl(\displaystyle\frac{b-a}{2}\biggr)^2-x^2}\biggr)^2-\biggl(\displaystyle\frac{a+b}{2}- \sqrt{\biggl(\displaystyle\frac{b-a}{2}\biggr)^2-x^2}\biggr)^2\biggr]dx\)
\(=4(a+b)\pi\displaystyle\int_{0}^{\frac{b-a}{2}} \sqrt{\biggl(\displaystyle\frac{b-a}{2}\biggr)^2-x^2}dx\)
\(=4\pi(a+b)\times \displaystyle\frac{1}{4}\times \biggl(\displaystyle\frac{b-a}{2}\biggr)^2 \times \pi\) \(\cdots\) 積分部分は円の面積の\(\displaystyle\frac{1}{4}\)
\(=\displaystyle\frac{1}{4}\pi^2(a+b)(b-a)^2\)
パップス=ギュルダンの定理
高校数学では裏技公式として有名なこの公式を使うと一瞬で答えが出てきます。
この定理はある図形を図形外の軸まわりに回してできる体積を求める公式で
「\(体積=図形の面積\times 重心の動いた距離\)」で求まる。今の場合
\(V=S\times L=\pi\biggl(\displaystyle\frac{b-a}{2}\biggr)^2 \times \pi(a+b)\)\(=\displaystyle\frac{1}{4}\pi^2(a+b)(b-a)^2\)