目次
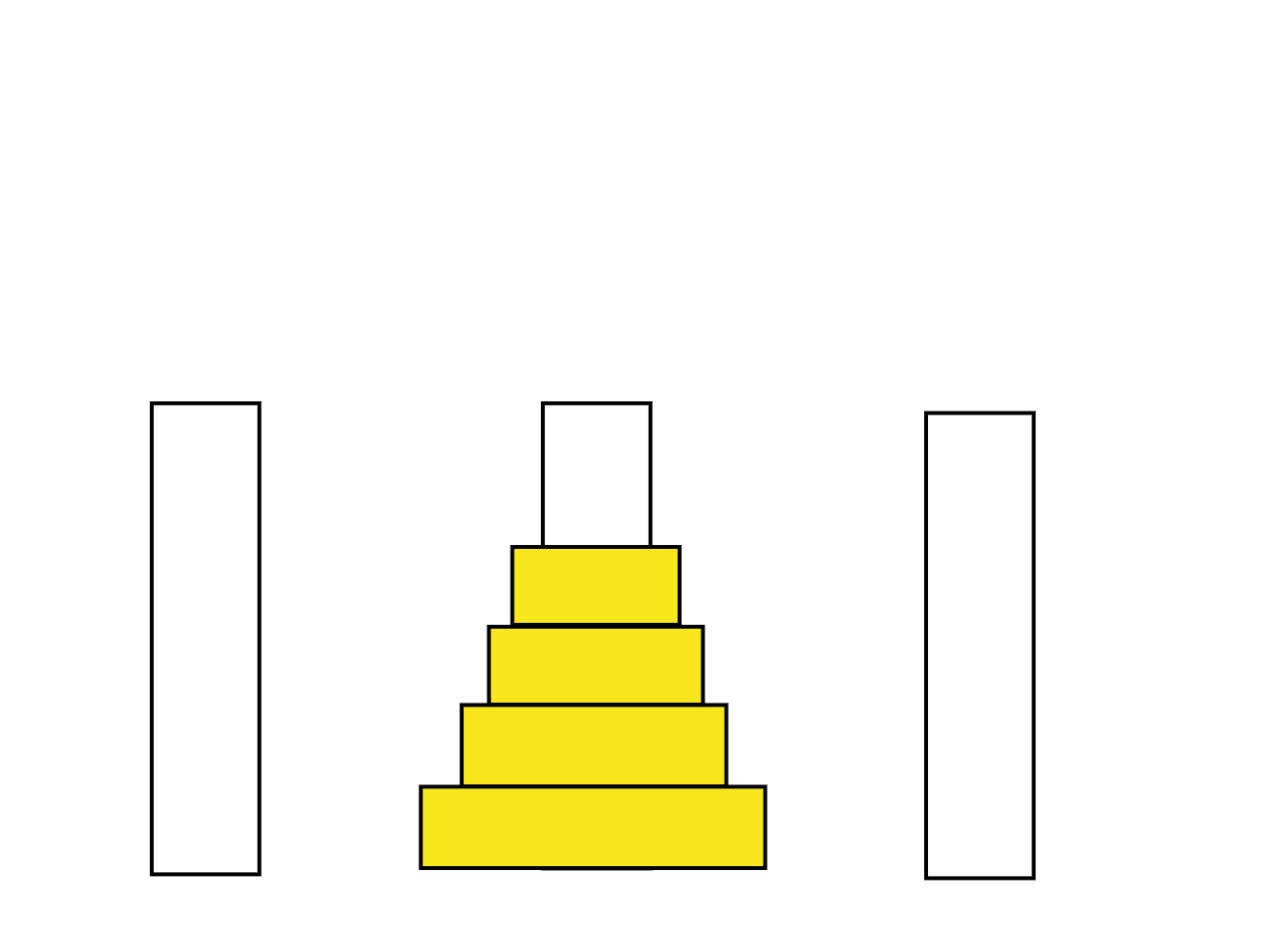
ハノイの塔
必要なもの
1、3本の柱
2、n枚の大きさの異なる円盤
ルール
1、上にある円盤が下のものより常に小さくなるようにする。
2、動かせるのは一度に1枚ずつ。
3、常に円盤は柱にあること。
目標
・中央(端でも良いですが)の柱にあるn枚の円盤を別の柱にすべて移す。
求めるもの
この条件のもとn枚の円盤を移すとき最短何手は? という問題です。
知らないと取っ掛かりが難しいかもしれないですね。
高校で習う漸化式! 使って求めていきます。
計算
n枚の時の最短手数を \(a_{n}\)とおく。
(n+1)枚の時との関係を調べる。
・動かし方
①まずn枚を移動させる …… (\(a_{n}\) 手)
②残り一枚を別の柱に移動させる。 …… (1 手)
③再びn枚を移動させる。 ……(\(a_{n}\) 手)
つまり漸化式としては \(a_{n+1}=2a_{n}+1\) となる。
これは \(a_{n+1}+1=2(a_{n}+1)\) と変形できる。
また、\(a_{1}=1\) より
\(a_{n}+1\) は初項2、公比2の等比数列。
よって、\(a_{n}+1=2^{n}\)
これよりn枚の時の総手数は \(a_{n}=2^{n}-1\) となる。
例えば、5枚の円盤を移すとなると\(31\)手以上かかるというわけです。
※円盤の枚数(n)が増えるほど指数関数的に手数は必要になります。