[mathjax]
目次
モンキーハンティング問題
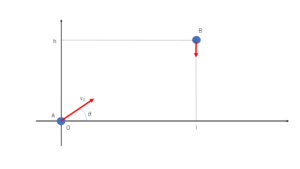
上のような状況を考える。
問題
① 衝突するときの\(\tan\theta\)を求めよ。
② 地面にぶつからない初速度の条件は?(\(\theta\)使わずに)
③ Bから見たAの速度は?
解答
1番
Aの運動
\(A_{x}=v_{0}\cos\theta\cdot t\)
\(A_{y}=v_{0}\sin\theta\cdot t-\displaystyle\frac{1}{2}gt^2\)
Bの運動
\(B_{x}=l\)
\(B_{y}=h-\displaystyle\frac{1}{2}gt^2\)
衝突時
\(A_{y}=B_{y}\)が成り立つ。その時刻は\(A_{x}=l\)から求められる。
\(t=\displaystyle\frac{l}{v_{0}\cos\theta}\)
\(h=v_{0}\sin\theta\cdot t=v_{0}\sin\theta\cdot\displaystyle\frac{l}{v_{0}\cos\theta}=l\tan\theta\)
\(\tan\theta=\displaystyle\frac{h}{l}\) が答え
これは衝突させるためにはAの発射方向をBに向ければよいということ。
また、初速度に依存しない所も注目すべき点。
2番
\(B_{y}=h-\displaystyle\frac{1}{2}gt^2>0\) から計算する。
\(h>\displaystyle\frac{1}{2}gt^2=\displaystyle\frac{1}{2}g\biggl(\displaystyle\frac{l^2}{v_{0}^2\cos^2\theta}\biggr)\)
\(=\displaystyle\frac{gl^2}{2v_{0}^2}(1+\tan^2\theta)=\displaystyle\frac{gl^2}{2v_{0}^2}\biggl(1+\displaystyle\frac{h^2}{l^2}\biggr)=\displaystyle\frac{g}{2v_{0}^2}(l^2+h^2)\)
より \(v_{0}>\sqrt{\displaystyle\frac{g(l^2+h^2)}{2h}}\)
3番
方向分けて考える。
\(v_{ax}-v_{bx}=v_{0}\cos\theta\)
\(v_{ay}-v_{by}=(v_{0}\sin\theta-gt)-(-gt)=v_{0}\sin\theta\)
つまり、BからみるとAが一直線に自分の方向に飛んでくるように見える。

