ビュフォンの針

内容

長さ\(a\)の針を長さ\(b\)の等間隔で書かれた線に落とした時に針が線と交わる確率を求める.

確率が \(\displaystyle\frac{2a}{b\pi }\) となり確率結果に円周率が入ってくることで有名.

導出方法

\(y\)：　針の中心から最も近い線までの距離。

\(\theta\)　：平行線と針のなす角。

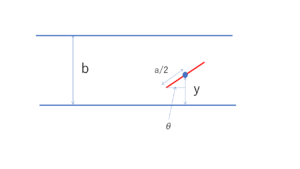
図のように変数設定.\( 0 \leq y \leq \displaystyle\frac{b}{2}\) , \( 0 \leq \theta < \displaystyle\frac{\pi}{2}\)に範囲を限る.（対称性があるのでここだけ考える）

縦の長さの関係に注目すると,

針と交わる　⇔　\( y \leq \displaystyle\frac{a}{2} \sin \theta\)　　

適当に投げるということは\(θ-y\) 平面の上記の範囲に一点を指定することになります.

全体の範囲　　\( 0 \leq y \leq \displaystyle\frac{b}{2}\) 、\( 0 \leq \theta < \displaystyle\frac{\pi}{2}\)

求める範囲　　\( y \leq \displaystyle\frac{a}{2} \sin \theta\)　

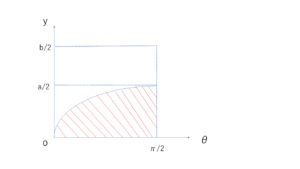
一番大きな四角形が全事象、赤斜線部分が交わる時です.\( y \leq \displaystyle\frac{a}{2} \sin \theta\)　より面積の比が確率に相当するので計算すると,

\(\displaystyle\frac{\displaystyle\frac{a}{2}\displaystyle\int_{0}^{\frac{\pi}{2}}\sin \theta d\theta}{\displaystyle\frac{\pi}{2}\cdot\displaystyle\frac{b}{2}}=\displaystyle\frac{2a}{b\pi }\)　