[mathjax]
目次
カージオイドとは
極座標表示が\(r=a(1+\cos\theta)\) で書ける軌跡の曲線。
軌跡が心臓の形に似ているため、別名を心臓形という。
イメージ画像(座標目盛りは\(a=1\)の時。)
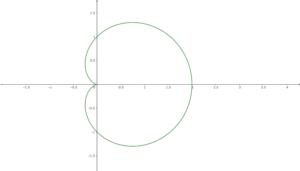
媒介変数表示
\(x=r\cos\theta=a\cos\theta(1+\cos\theta)\)
\(y=r\sin\theta=a\sin\theta(1+\cos\theta)\)
\(\theta\)を\(2\pi-\theta\)にすると\(x\)はそのまま、\(y\)は符号が入れ替わるので\(x\)軸対称になっている。(面積計算、長さ計算が少し楽にできる)
以下の計算で使うので準備
\(\displaystyle\frac{dx}{d\theta}=-a\sin\theta(1+2\cos\theta)\)
\(\displaystyle\frac{dy}{d\theta}=a(2\cos^2\theta+\cos\theta-1)\)
結論から言うと、面積が \(\displaystyle\frac{3}{2}\pi a^2\)で、長さが\(8a\) 。
媒介変数消去
媒介変数を消去できることにはできるが、ふつうは媒介変数表示のまま使用する。
媒介変数表示は
\(x=r\cos\theta=a\cos\theta(1+\cos\theta)\)
\(y=r\sin\theta=a\sin\theta(1+\cos\theta)\)
であり、二乗して二式を足すと
\(x^2+y^2=a^2(1+\cos\theta)^2\)
ここから\(|\cos\theta|\leq 1\)であることに注意すると
\(\cos\theta=-1+\displaystyle\frac{\sqrt{x^2+y^2}}{a}\)
これを\(x=a\cos\theta(1+\cos\theta)\)に代入すると
\(x=-\sqrt{x^2+y^2}+\displaystyle\frac{x^2+y^2}{a}\)
整理すると以下のようになる。
\((x^2+y^2-ax)^2=a^2(x^2+y^2)\)
面積
媒介変数表示でも極座標表示のままでも計算できる。
媒介変数表示
※一番\(x\)座標が小さい点は \(\displaystyle\frac{dx}{d\theta}=-a\sin\theta(1+2\cos\theta)=0\) から求められる。
\(0\leq \theta\leq 2\pi\)にかけて反時計回りに一周する。
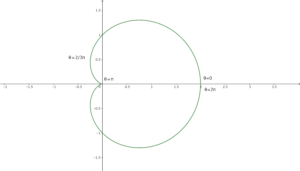
上半面(\(0\leq \theta\leq \pi\))の面積を求めてそれを二倍する。
\(S=2\displaystyle\int_{-\frac{1}{4}a}^{2a} y dx-2\displaystyle\int_{-\frac{1}{4}a}^{0} y dx\)
※第二項は余分な所(\(-\displaystyle\frac{a}{4}\leq x\leq 0\)で曲線より下の部分)を引いている。
\(=2\displaystyle\int_{\frac{2}{3}\pi}^{0} -a(1+\cos\theta)\sin\theta\times a\sin\theta(1+2\cos\theta) d\theta\)
\(-2\displaystyle\int_{\frac{2}{3}\pi}^{\pi} -a(1+\cos\theta)\sin\theta\times a\sin\theta(1+2\cos\theta) d\theta\)
\(=2\displaystyle\int_{0}^{\pi} a(1+\cos\theta)\sin\theta\times a\sin\theta(1+2\cos\theta) d\theta\)
\(=2a^2 \displaystyle\int_{0}^{\pi} (-2\cos^4 \theta-3\cos^3 \theta+\cos^2 \theta+3\cos\theta+1)d\theta\)
\(=2a^2 \displaystyle\int_{0}^{\pi} \biggl( -2\cdot \displaystyle\frac{\cos 4\theta+4\cos 2\theta+3}{8}-3\cdot\displaystyle\frac{\cos 3\theta+3\cos\theta}{4}\)
\(+\displaystyle\frac{1+\cos 2\theta}{2}+3\cos\theta+1\biggr)d\theta\)
※第一項は\(\cos 4\theta=2\cos^2 2\theta-1=2(2\cos^2\theta-1)^2-1\)から計算。
\(=2a^2 \displaystyle\int_{0}^{\pi}\biggl(-\displaystyle\frac{1}{4}\cos 4\theta-\displaystyle\frac{3}{4}\cos 3\theta-\displaystyle\frac{1}{2}\cos 2\theta+\displaystyle\frac{3}{4}\cos\theta+\displaystyle\frac{3}{4}\biggr)d\theta\)
\(=\biggl[-\displaystyle\frac{1}{16}\sin 4\theta-\displaystyle\frac{1}{4}\sin 3\theta-\displaystyle\frac{1}{4}\sin 2\theta+\displaystyle\frac{3}{4}\sin\theta+\displaystyle\frac{3}{4}\theta\biggr]_{0}^{\pi}\)
\(=\displaystyle\frac{3}{2}\pi a^2\)
極座標表示
極座標表示の面積計算公式を使う。(記述なら略証があったほうが良い)
\(S=\displaystyle\frac{1}{2}\displaystyle\int_{0}^{2\pi} r^2 d\theta\)
\(=\displaystyle\frac{1}{2}\displaystyle\int_{0}^{2\pi} a^2(1+\cos\theta)^2 d\theta\)
\(=\displaystyle\frac{1}{2}a^2\displaystyle\int_{0}^{2\pi} \biggl(1+2\cos\theta+\displaystyle\frac{1+\cos 2\theta}{2}\biggr) d\theta\)
\(=\displaystyle\frac{1}{2}a^2\biggl[\displaystyle\frac{3}{2}\theta+2\sin\theta+\displaystyle\frac{1}{4}\sin 2\theta\biggr]_{0}^{2\pi}\)
\(=\displaystyle\frac{3}{2}\pi a^2\)
長さ
媒介変数表示でも極座標表示のままでも計算できる。
媒介変数表示
正攻法のやり方。上半面(\(0\leq \theta\leq \pi\))の長さを求めてそれを二倍する。
\(L=2\displaystyle\int_{0}^{\pi}\sqrt{\biggl(\displaystyle\frac{dx}{d\theta}\biggr)^2+\biggl(\displaystyle\frac{dy}{d\theta}\biggr)^2} d\theta\)
\(=2\displaystyle\int_{0}^{\pi}\sqrt{a^2\sin^2 \theta(1+2\cos\theta)^2+a^2(2\cos^2\theta+\cos\theta-1)^2}d\theta\)
\(=2a\displaystyle\int_{0}^{\pi}\biggl|2\cos\displaystyle\frac{\theta}{2}\biggr| d\theta\)
\(=4a\displaystyle\int_{0}^{\pi}\cos\displaystyle\frac{\theta}{2} d\theta\)
※ \(0\leq\theta\leq\pi\) で \(\cos\displaystyle\frac{\theta}{2}\geq 0\)
\(=\biggl[8a\sin\displaystyle\frac{\theta}{2}\biggr]_{0}^{\pi}\)
\(=8a\)
極座標表示
極座標表示の曲線長計算公式を使う。(記述なら略証があったほうが良い)
\(L=2\displaystyle\int_{0}^{\pi} \sqrt{r^2+\biggl(\displaystyle\frac{dr}{d\theta}\biggr)^2}d\theta\)
\(=2\displaystyle\int_{0}^{\pi} \sqrt{a^2(1+\cos\theta)^2+a^2\sin^2\theta}d\theta\)
\(=2a\displaystyle\int_{0}^{\pi} \sqrt{2(1+\cos\theta)}d\theta\)
\(=4a\displaystyle\int_{0}^{\pi}\cos\displaystyle\frac{\theta}{2} d\theta\)
※ \(0\leq\theta\leq\pi\) で \(\cos\displaystyle\frac{\theta}{2}\geq 0\)
\(=\biggl[8a\sin\displaystyle\frac{\theta}{2}\biggr]_{0}^{\pi}\)
\(=8a\)

