[mathjax]
目次
レムニスケート
レム二スケートは極方程式が\(r^2=2a^2\cos 2\theta\)で表される図形。連珠形とも呼ばれる。
以下の画像のような軌跡になる。
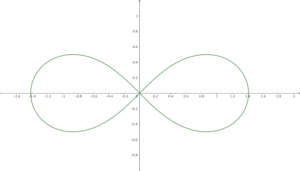
直交座標系に変換すると \((x^2+y^2)^2=2a^2(x^2-y^2)\) になる。
※この形から、\(x\)、\(y\)軸対称であることが分かる。
※「\(x^2+y^2=r^2\)」と「\(x^2-y^2=r^2(\cos^2\theta-\sin^2\theta)=r^2\cos 2\theta\)」よりわかる。
結論から言うと面積が \(2a^2\) で長さが\(\sqrt{2\pi}a\displaystyle\frac{\Gamma{\biggl(\displaystyle\frac{1}{4}\biggr)}}{\Gamma\biggl(\displaystyle\frac{3}{4}\biggr)}\)
以下、レム二スケートの面積と長さを媒介変数表示及び極座標表示で計算していきます。最後にレム二スケート周率について軽く触れました。
媒介変数表示
\(x=r\cos\theta=\sqrt{2}a\cos\theta\sqrt{\cos 2\theta}\)
\(y=r\sin\theta=\sqrt{2}a\sin\theta\sqrt{\cos 2\theta}\)
以下の計算で使うので準備
\(\displaystyle\frac{dx}{d\theta}=-\sqrt{2}a\displaystyle\frac{\sin 3\theta}{\sqrt{\cos 2\theta}}\)
\(\displaystyle\frac{dy}{d\theta}=\sqrt{2}a\displaystyle\frac{\cos 3\theta}{\sqrt{\cos 2\theta}}\)
\(\displaystyle\frac{dx}{d\theta}=\sqrt{2}a\biggl[\displaystyle\frac{1}{2}(\cos 2\theta)^{-\frac{1}{2}}\times(-2\sin 2\theta\cos\theta)+\sqrt{2}a\sqrt{\cos 2\theta}(-\sin\theta)\biggr]\)
\(=-\displaystyle\frac{\sqrt{2}a}{\sqrt{\cos 2\theta}}(\cos\theta\sin 2\theta+\sin\theta\cos 2\theta)\)
\(=-\sqrt{2}a\displaystyle\frac{\sin 3\theta}{\sqrt{\cos 2\theta}}\) ※分子は加法定理で合成
※\(y\)についても同じ要領でできる
面積
媒介変数表示でも極座標表示のままでも計算できる。極座標のままの方が簡単。
極座標表示
極座標表示の面積計算公式を使う。(記述なら略証があったほうが良い)
\(x\)軸と\(y\)軸対称なので第一象限の4倍を計算する。
\(S=4\times \displaystyle\frac{1}{2}\displaystyle\int_{0}^{\frac{\pi}{4}} r^2 d\theta\)
\(=2\displaystyle\int_{0}^{\frac{\pi}{4}} 2a^2\cos 2\theta d\theta\)
\(=4a^2\biggl[\displaystyle\frac{1}{2}\sin 2\theta\biggr]_{0}^{\frac{\pi}{4}}\)
\(=2a^2\)
媒介変数表示
媒介変数表示の状態でできなくもないですが、計算量が多くなる。
\(S=4\times \displaystyle\int_{0}^{2a^2} y dx\)
\(=4\times\displaystyle\int_{\frac{\pi}{4}}^{0} \sqrt{2}a\sqrt{\cos 2\theta}\sin\theta\times \biggl(-\sqrt{2}a \displaystyle\frac{\sin 3\theta}{\sqrt{\cos 2\theta}}\biggr) d\theta\)
\(=8a^2\displaystyle\int_{0}^{\frac{\pi}{4}} \sin\theta\sin 3\theta d\theta\)
\(=8a^2\displaystyle\int_{0}^{\frac{\pi}{4}} \biggl(\displaystyle\frac{1}{2}\cos 2\theta-\displaystyle\frac{1}{2}\cos 4\theta\biggr) d\theta\)
※三角関数の積和公式
\(=8a^2\biggl[\displaystyle\frac{1}{4}\sin 2\theta-\displaystyle\frac{1}{8}\sin 4\theta\biggr]_{0}^{\frac{\pi}{4}}\)
\(=2a^2\)
長さ
媒介変数表示でも極座標表示のままでも計算できる。
極座標表示
極座標表示の長さ計算公式を使う。(記述なら略証があったほうが良い)
x軸とy軸対称なので第一象限の4倍を計算する。
\(L=4\displaystyle\int_{0}^{\frac{\pi}{4}} \sqrt{r^2+\biggl(\displaystyle\frac{dr}{d\theta}\biggr)^2}d\theta\)
\(=4\displaystyle\int_{0}^{\frac{\pi}{4}} \sqrt{2a^2\cos 2\theta+2a^2\displaystyle\frac{\sin^2 2\theta}{\cos 2\theta}}d\theta\)
\(=4\sqrt{2}a\displaystyle\int_{0}^{\frac{\pi}{4}}\displaystyle\frac{d\theta}{\sqrt{\cos 2\theta}}\)
ここで \(t=\tan\theta\)とおく。\(\displaystyle\frac{dt}{d\theta}=\displaystyle\frac{1}{\cos^2\theta}=1+t^2\) なので
\(=4\sqrt{2}a\displaystyle\int_{0}^{1}\displaystyle\frac{1}{\sqrt{\displaystyle\frac{2}{1+t^2}-1}}\cdot \displaystyle\frac{dt}{1+t^2}\)
\(=4\sqrt{2}a\displaystyle\int_{0}^{1}\displaystyle\frac{dt}{\sqrt{1-t^4}}\)
\(u=t^4\)とおく。\(\displaystyle\frac{dt}{du}=\displaystyle\frac{1}{4}u^{-\frac{3}{4}}\)なので
\(=\sqrt{2}a\displaystyle\int_{0}^{1} u^{\frac{1}{4}-1} (1-u)^{\frac{1}{2}-1}du\)
\(=\sqrt{2}a B\biggl(\displaystyle\frac{1}{4}, \displaystyle\frac{1}{2}\biggr)\)
\(=\sqrt{2\pi}a\displaystyle\frac{\Gamma{\biggl(\displaystyle\frac{1}{4}\biggr)}}{\Gamma\biggl(\displaystyle\frac{3}{4}\biggr)}\)
媒介変数表示
第一象限の4倍と考える。途中からは上と同じ計算になる。
\(L=4\displaystyle\int_{0}^{\frac{\pi}{4}}\sqrt{\biggl(\displaystyle\frac{dx}{d\theta}\biggr)^2+\biggl(\displaystyle\frac{dy}{d\theta}\biggr)^2} d\theta\)
\(=4\displaystyle\int_{0}^{\frac{\pi}{4}} \sqrt{2}a\sqrt{\displaystyle\frac{\sin^2 3\theta}{\cos 2\theta}+\displaystyle\frac{\cos^2 3\theta}{\cos 2\theta}} d\theta\)
\(=4\sqrt{2}a\displaystyle\int_{0}^{\frac{\pi}{4}}\displaystyle\frac{d\theta}{\sqrt{\cos 2\theta}}\)
ここで \(t=\tan\theta\)とおく。\(\displaystyle\frac{dt}{d\theta}=\displaystyle\frac{1}{\cos^2\theta}=1+t^2\) なので
\(=4\sqrt{2}a\displaystyle\int_{0}^{1}\displaystyle\frac{1}{\sqrt{\displaystyle\frac{2}{1+t^2}-1}}\cdot \displaystyle\frac{dt}{1+t^2}\)
\(=4\sqrt{2}a\displaystyle\int_{0}^{1}\displaystyle\frac{dt}{\sqrt{1-t^4}}\)
\(u=t^4\)とおく。\(\displaystyle\frac{dt}{du}=\displaystyle\frac{1}{4}u^{-\frac{3}{4}}\)なので
\(=\sqrt{2}a\displaystyle\int_{0}^{1} u^{\frac{1}{4}-1} (1-u)^{\frac{1}{2}-1}du\)
\(=\sqrt{2}a B\biggl(\displaystyle\frac{1}{4}, \displaystyle\frac{1}{2}\biggr)\)
\(=\sqrt{2\pi}a\displaystyle\frac{\Gamma{\biggl(\displaystyle\frac{1}{4}\biggr)}}{\Gamma\biggl(\displaystyle\frac{3}{4}\biggr)}\)
レム二スケート周率
おまけの話です。レム二スケート周率は、円でいう所の円周率に対応する概念になります。
\(a=\displaystyle\frac{1}{\sqrt{2}}\)の場合のレム二スケートは\(r^2=\cos 2\theta\)になり、長さは極座標の長さ計算の途中から
\(L_{レ}=4\displaystyle\int_{0}^{\frac{\pi}{4}} \displaystyle\frac{d\theta}{\sqrt{\cos 2\theta}}=4\displaystyle\int_{0}^{1} \displaystyle\frac{dr}{\sqrt{1-r^4}}\)
途中計算
\(\displaystyle\frac{dr}{d\theta}=-\sqrt{\cos 2\theta}\tan 2\theta=-\sqrt{r^2}\sqrt{\displaystyle\frac{1}{r^4}-1}\)
なので
\(\displaystyle\frac{d\theta}{dr}=-\sqrt{\displaystyle\frac{r^2}{1-r^4}}\)
ここで単位円(レム二スケートの時と対応させている)の場合を考えると
\(L_{円}=4\displaystyle\int_{0}^{1}\displaystyle\frac{dx}{\sqrt{1-x^2}}\)
\(L_{円}=2\pi\)なので、レム二スケートに対応させて考えると
\(L_{レ}=2\varpi\)とおくとよく、このとき
\(\varpi=2\displaystyle\int_{0}^{1} \displaystyle\frac{dr}{\sqrt{1-r^4}}=\sqrt{2\pi}\times\displaystyle\frac{1}{\sqrt{2}}\displaystyle\frac{\Gamma{\biggl(\displaystyle\frac{1}{4}\biggr)}}{\Gamma\biggl(\displaystyle\frac{3}{4}\biggr)}\)
\(=\displaystyle\frac{\pi\Gamma{\biggl(\displaystyle\frac{1}{4}\biggr)}}{\Gamma\biggl(\displaystyle\frac{3}{4}\biggr)}\)
となり、これを「レムニスケート周率」という。