[mathjax]
目次
スーパーボール
スーパーボールが地面で跳ね返った時の運動を調べる。
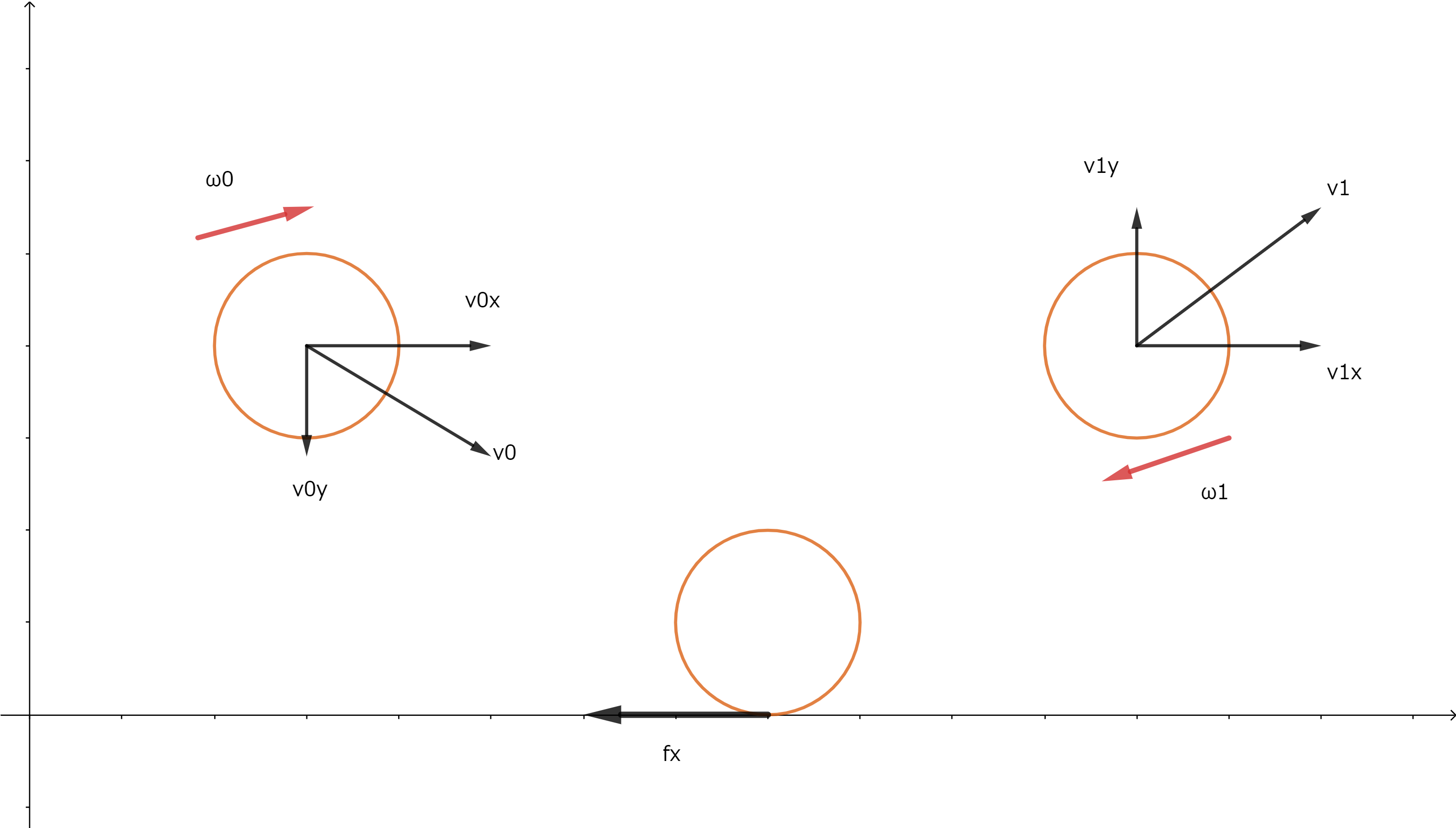
跳ねる前 速度\(v_{0}\)、角速度\(\omega_{0}\)
跳ねた後 速度\(v_{1}\)、角速度\(\omega_{1}\)
跳ねる時の変換計算
運動量と力積
\(x\)軸方向に関して
\(M(v_{1x}-v_{0x})=\displaystyle\int_{0}^{\Delta t} f_{x} dt=-f_{x}\Delta t\) \(\cdots\) ①
慣性モーメント
\(I(\omega_{1}-\omega_{0})=-a\displaystyle\int_{0}^{\Delta t} f_{x} dt=-a f_{x} \Delta t\) \(\cdots\) ②
力学的エネルギー保存の法則
\(x\)方向に関して
\(\displaystyle\frac{1}{2}Mv_{0x}^2+\displaystyle\frac{1}{2}I\omega_{0}^2=\displaystyle\frac{1}{2}Mv_{1x}^2+\displaystyle\frac{1}{2}I\omega_{1}^2\)
変形すると \(M(v_{1x}^2-v_{0x}^2)=-I(\omega_{1}^2-\omega_{0}^2)\) \(\cdots\) ③
計算
①と②より \(M(v_{1x}-v_{0x})=\displaystyle\frac{I}{a}(\omega_{1}-\omega_{0})\) \(\cdots\) ④
\(\displaystyle\frac{③}{④}\)より \(v_{1x}+v_{0x}=-a(\omega_{1}+\omega_{0})\) \(\cdots\) ⑤
④でスーパーボールは球であることから\(I=\displaystyle\frac{2}{5}Ma^2\)を代入。
\(v_{1x}+\displaystyle\frac{2}{5}a\omega_{1}=v_{0x}+\displaystyle\frac{2}{5}a\omega_{0}\) \(\cdots\) ⑥
⑤と⑥より(※\(v_{1x},a\omega_{1}\)で表すと行列形式に書ける)
\(\left(\begin{array}{c} v_{1x} \\ a\omega_{1} \end{array} \right) =\displaystyle\frac{1}{7}\left(\begin{array}{cc} 3 & 4 \\ 10 & -3\end{array}\right)\left(\begin{array}{c} v_{0x} \\ a\omega_{0} \end{array} \right) \)
これが、跳ねた時の変換になる。
例
その1
\(v_{0x}=0\)のとき
\(\left(\begin{array}{c} v_{1x} \\ a\omega_{1} \end{array} \right) =\displaystyle\frac{1}{7}\left(\begin{array}{cc} 3 & 4 \\ 10 & -3\end{array}\right)\left(\begin{array}{c} 0 \\ a\omega_{0} \end{array} \right) \)
より
\(v_{1x}=\displaystyle\frac{4}{7}a\omega_{0}\)、\(\omega_{1}=-\displaystyle\frac{3}{7}\omega_{0}\)
つまり、\(\omega\)は右回転してるので、右方向にボールは飛ぶ(当たり前ですが笑)
2回目のバウンドを考える。先ほどの結果を右辺に代入すると
\(\left(\begin{array}{c} v_{2x} \\ a\omega_{2} \end{array} \right) =\displaystyle\frac{1}{7}\left(\begin{array}{cc} 3 & 4 \\ 10 & -3\end{array}\right)\left(\begin{array}{c} \displaystyle\frac{4}{7}a\omega_{0} \\ -\displaystyle\frac{3}{7}a\omega_{0} \end{array} \right) \)
\(v_{2x}=0\)、\(\omega_{2}=\omega_{0}\)となる。
つまり、真上に跳ね上がることになる!また、この状況は最初の状況と同じなので、この場合の運動は同じ運動が繰り返されることとなる。
その2
\(\omega_{0}=0\)のとき
\(\left(\begin{array}{c} v_{1x} \\ a\omega_{1} \end{array} \right) =\displaystyle\frac{1}{7}\left(\begin{array}{cc} 3 & 4 \\ 10 & -3\end{array}\right)\left(\begin{array}{c} v_{0x} \\ 0 \end{array} \right) \)
より
\(v_{1x}=\displaystyle\frac{3}{7}v_{0x}\)、\(\omega_{1}=\displaystyle\frac{10}{7a}v_{0x}\)
先ほどと同様に2回目のバウンドを考える。先ほどの結果を右辺に代入すると
\(\left(\begin{array}{c} v_{2x} \\ a\omega_{2} \end{array} \right) =\displaystyle\frac{1}{7}\left(\begin{array}{cc} 3 & 4 \\ 10 & -3\end{array}\right)\left(\begin{array}{c} \displaystyle\frac{3}{7}v_{0x} \\ \displaystyle\frac{10}{7}v_{0x} \end{array} \right) \)
これを解くと\(v_{2x}=v_{0x}\)、\(\omega_{2}=0\)となる。
一般
変換行列を\(T\)とおくと
\(T=\displaystyle\frac{1}{7}\left(\begin{array}{cc} 3 & 4 \\ 10 & -3\end{array}\right)\)
\(T^2=\left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right)\)
となるので、スーパーボールの運動では、初期条件によらず二回跳ねると元の条件に戻るので、同じ運動を繰り返すことになる。