中線定理 | 日々の日記

中線定理とは

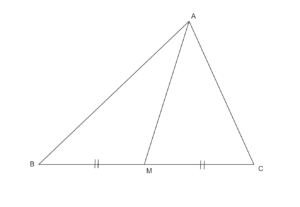
図において、$AB^2+AC^2=2(AM^2+BM^2)$が成り立つ。これを中線定理という。

$BM=CM$であり、$AM$のことを中線と呼ぶので、中線定理という。

△ABMと△ACMにおいて余弦定理を適用する。（$\angle AMC=\theta$とおく。）

$AB^2=AM^2+BM^2-2AM\cdot BM\cdot \cos (\pi-\theta)$

$AC^2=AM^2+CM^2-2AM\cdot CM\cdot \cos \theta$

$BM=CM$を考慮して、辺々足すと　

$AB^2+AC^2=2(AM^2+BM^2)$

※$\cos(\pi-\theta)=-\cos\theta$です。

座標設定する方法です。Mを原点にとり、$B(-c,0)、C(c,0)$としても一般性を失わない。

$A(a,b)$とすると

$左辺=AB^2+AC^2=(a+c)^2+b^2+(a-c)^2+b^2=2(a^2+b^2+c^2)$

$右辺=2(AM^2+BM^2)=2((a^2+b^2)+c^2)$

となり、一致する。