[mathjax]
目次
フレネル積分
\(\displaystyle\int_{-\infty}^{\infty}\sin x^2 dx=\displaystyle\int_{-\infty}^{\infty}\cos x^2 dx=\sqrt{\displaystyle\frac{\pi}{2}}\)
※ \(\sin x^2\) は \(\sin^2 x\) とは別物です。
イメージ
ガウス積分を使用。(厳密ではないですが分かりやすいかもしれないです)
$$\displaystyle\int_{-\infty}^{\infty}e^{ix^2}=\sqrt{\displaystyle\frac{\pi}{-i}}=\sqrt{\pi i}=\sqrt{\displaystyle\frac{\pi}{2}}(1+i)$$
\(\sqrt{\pi i}=a+bi\)とでも置いて計算すれば出てくる。また、
$$\displaystyle\int_{-\infty}^{\infty}e^{ix^2}=\displaystyle\int_{-\infty}^{\infty} \cos x^2+i\displaystyle\int_{-\infty}^{\infty}\sin x^2$$
実部と虚部を比較すると
$$\displaystyle\int_{-\infty}^{\infty}\sin x^2 dx=\displaystyle\int_{-\infty}^{\infty}\cos x^2 dx=\sqrt{\displaystyle\frac{\pi}{2}}$$
証明
$f(z)=e^{iz^2}$を$\displaystyle\frac{\pi}{4}$の扇形で複素積分します。
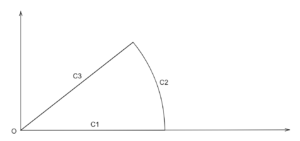
$$\displaystyle\int_{0}^{\infty} e^{ix^2} dx+\displaystyle\int_{\mathrm{C}_{2}} e^{iz^2} dz+\displaystyle\int_{\mathrm{C}_{3}} e^{iz^2} dz=0$$
\(C_{2}\)の経路
$$\displaystyle\int_{\mathrm{C}_{2}} e^{iz^2} dz\to 0$$
\(C_{3}\)の経路
$z=e^{\frac{i\pi}{4}}x$と変換する。
$$\displaystyle\int_{\mathrm{C}_{3}} e^{iz^2} dz=\displaystyle\int_{\infty}^{0} e^{-x^2}e^{\frac{i\pi}{4}} dx=-\left(\displaystyle\frac{1+i}{\sqrt{2}}\right)\displaystyle\frac{\sqrt{\pi}}{2}$$
まとめ
これらの結果を代入すると以下の式が得られる。
$$\displaystyle\int_{0}^{\infty} \cos x^2 dx+i\displaystyle\int_{0}^{\infty} \sin x^2 dx=\left(\displaystyle\frac{1+i}{\sqrt{2}}\right)\displaystyle\frac{\sqrt{\pi}}{2}$$
実部、虚部を比較して計算し、積分範囲を倍にするとフレネル積分が得られる。
$$\displaystyle\int_{-\infty}^{\infty}\sin x^2 dx=\displaystyle\int_{-\infty}^{\infty}\cos x^2 dx=\sqrt{\displaystyle\frac{\pi}{2}}$$

