目次
楕円 接線直交
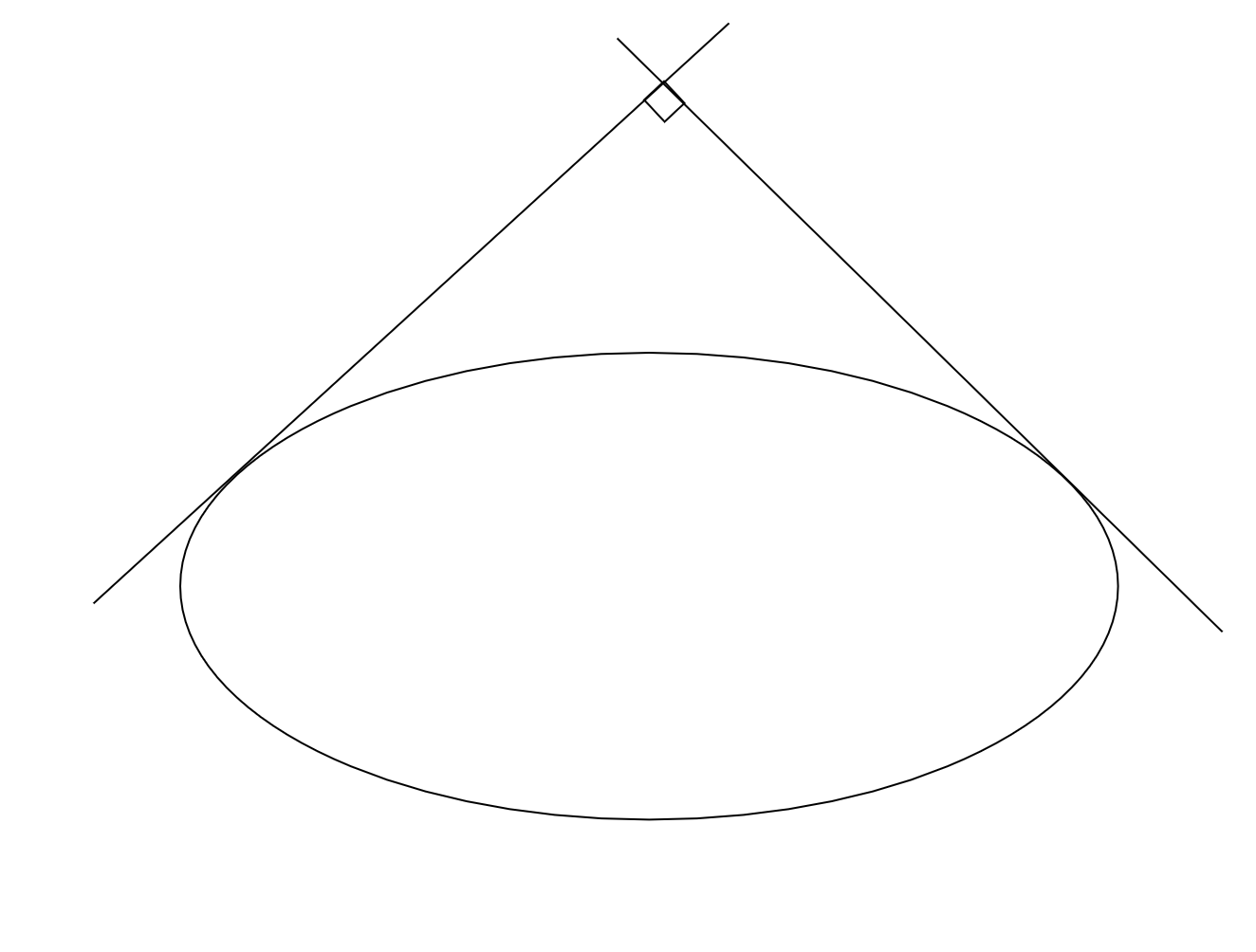
楕円の直交する2本の接線の交点の軌跡に関する話です。
楕円のある二点での接線が直交する場合の交点の軌跡は準円と呼ばれる円になります。
証明
交点を$P(X,Y)$とする。傾きを$m$とおくと、Pを通る直線の方程式は
$X\neq a$のとき
$y=m(x-X)+Y$となる。この直線が楕円と接することから楕円方程式$\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1$と連立したときの判別式が0となる。
$\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{(m(x-X)+Y)^2}{b^2}=1$
整理すると
$(a^2m^2+b^2)x^2-2a^2 m(Y-mX)x+(Y-mX)^2a^2-a^2b^2=0$
これの判別式が0なのでそれを解くと、
$D=4a^2b^2((a^2-X^2)m^2+2XYm+b^2-Y^2)=0$
$(a^2-X^2)m^2+2XYm+b^2-Y^2=0$となるが、ここで接線が直交する条件からこの方程式の2解を$m_{1},m_{2}$とすると$m_{1}m_{2}=-1$となる。
解と係数の関係を用いると、$\displaystyle\frac{b^2-Y^2}{a^2-X^2}=-1$ となり、整理すると
$X^2+Y^2=a^2+b^2$となる。これは半径$\sqrt{a^2+b^2}$の円で準円と呼ばれる。
$x=\pm a$のとき
このときは$y=\pm b$となるので、上で求めた円に入っている。