[mathjax]
目次
確率密度関数
$\mu$を平均、$\sigma$を標準偏差とする。確率密度関数は
$f(x)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
$\mu=0,\sigma=1$のものは標準正規分布という。
期待値
$E[X]=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} x \mathrm{exp}\biggl[-\displaystyle\frac{(x-\mu)^2}{2\sigma^2}\biggr] dx$
$=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} (x-\mu) \mathrm{exp}\biggl[-\displaystyle\frac{(x-\mu)^2}{2\sigma^2}\biggr] dx+\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} \mu \mathrm{exp}\biggl[-\displaystyle\frac{(x-\mu)^2}{2\sigma^2}\biggr] dx$
$=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} x \mathrm{exp}\biggl[-\displaystyle\frac{x^2}{2\sigma^2}\biggr] dx+\mu$
$= \mu$
※第一項は奇関数なので消えます。
分散
分散は以下のようになる。
$\mathrm{Var}(X)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} (x-\mu)^2 \mathrm{exp}\biggl[-\displaystyle\frac{(x-\mu)^2}{2\sigma^2}\biggr] dx$
$=\biggl[-\displaystyle\frac{\sigma^2}{\sqrt{2\pi\sigma^2}} (x-\mu) \mathrm{exp}\biggl[-\displaystyle\frac{(x-\mu)^2}{2\sigma^2}\biggr]\biggr]_{-\infty}^{\infty}+\displaystyle\frac{\sigma^2}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} \mathrm{exp}\biggl[-\displaystyle\frac{(x-\mu)^2}{2\sigma^2}\biggr]dx$
$= \sigma^2$
積率母関数
$M_{X}(t)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} e^t \mathrm{exp}\biggl[-\displaystyle\frac{(x-\mu)^2}{2\sigma^2}\biggr] dx$
$=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} \mathrm{exp}\biggl[-\displaystyle\frac{1}{2\sigma^2}\left((x-(\mu+t\sigma^2))^2-2\mu t\sigma^2-t^2\sigma^4 \right)\biggr] $
$=e^{\mu t+\frac{\sigma^2 t^2}{2}}$
グラフ
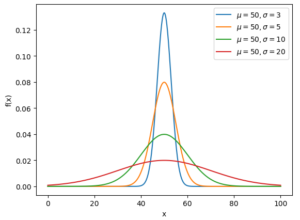
code


