目次
ラングレーの問題
幾何学の有名問題です。
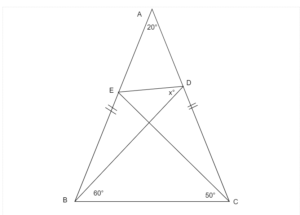
以下の図において、$x^{\circ}$を求める。△ABCは二等辺三角形です。
解答
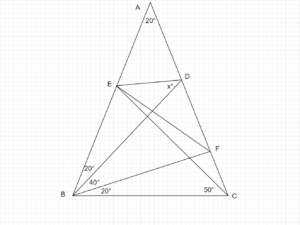
AC上にBC=BFとなるようにFを取る。
△BCE
△BCEを考えると、$\angle BCE=\angle BEC=50^{\circ}$なので△BCEは二等辺三角形。
すなわちBC=BE。
△BEF
BC=BFとBC=BEなので、BE=BFで頂角が$60^{\circ}$なので正三角形。
△BCD
$\angle CBD=60^{\circ}$及び、$\angle BCD=80^{\circ}$なので
$\angle BDC=40^{\circ}$となる。
△BFD
$\angle FBD=\angle FDB=40^{\circ}$なので、BF=DFの二等辺三角形。
△DEF
今までのことをまとめると△DEFは、EF=DFの二等辺三角形となる。
$\angle DFE=40^{\circ}$なので、$\angle FDE=70^{\circ}$
$x=70^{\circ}-40^{\circ}=$$30^{\circ}$となる。

