sin15°の求め方

[mathjax]

 

$\sin 15^{\circ}$　求め方1

 

 

 

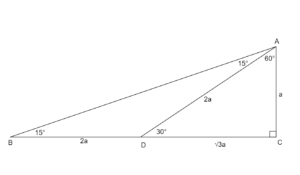
$15^{\circ}$と$75^{\circ}$の三角形ABCにおいてACを$a$とおく。

$\angle DAC=60^{\circ}$となるようにDを作り、補助線を引く。

 

$AD=2a$、$CD=\sqrt{3}a$となる。また、△DABは$\angle DAB=\angle DBA=15^{\circ}$なので

DB=DA$=2a$となる。

 

この図から、$\tan 15^{\circ}=\displaystyle\frac{1}{2+\sqrt{3}}=2-\sqrt{3}$

 

三平方の定理から、

AB=$\sqrt{1+(2+\sqrt{3})^2}a=\sqrt{8+2\sqrt{12}}a=(\sqrt{6}+\sqrt{2})a$

 

よって

$\sin 15^{\circ}=\displaystyle\frac{1}{\sqrt{6}+\sqrt{2}}=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}$

 

$\cos 15^{\circ}=\displaystyle\frac{2+\sqrt{3}}{\sqrt{6}+\sqrt{2}}=\displaystyle\frac{\sqrt{6}+\sqrt{2}}{4}$

 

$AB:BC:CA=4:(\sqrt{6}+\sqrt{2}):(\sqrt{6}-\sqrt{2})$という比率は有名なので覚えておいて損はないです。

 

 

$\sin 15^{\circ}$　求め方2

加法定理を使います。

 

$\sin 15^{\circ}$

$\sin 15^{\circ}=\sin (45^{\circ}-30^{\circ})=\sin 45^{\circ}\cos 30^{\circ}-\cos 45^{\circ}\sin 30^{\circ}$

$=\displaystyle\frac{1}{\sqrt{2}}\times\displaystyle\frac{\sqrt{3}}{2}-\displaystyle\frac{1}{\sqrt{2}}\times\displaystyle\frac{1}{2}$

$=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}$

 

$\cos 15^{\circ}$

$\cos 15^{\circ}=\cos (45^{\circ}-30^{\circ})=\cos 45^{\circ}\cos 30^{\circ}+\sin 45^{\circ}\sin 30^{\circ}$

$=\displaystyle\frac{1}{\sqrt{2}}\times\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{1}{\sqrt{2}}\times\displaystyle\frac{1}{2}$

$=\displaystyle\frac{\sqrt{6}+\sqrt{2}}{4}$

 

$\tan 15^{\circ}$

$\tan 15^{\circ}=\displaystyle\frac{\sin 15^{\circ}}{\cos 15^{\circ}}$$=2-\sqrt{3}$

 

 

まとめ

$15^{\circ}$関連の三角比をまとめます。ここから$75^{\circ}$の三角比もすぐに求めることが出来ます。