目次
未定乗数法
問題
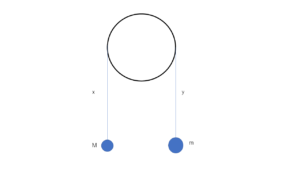
滑車にひもがかかっている。
左のひもの長さが\(x\)、右のひもの長さが\(y\)。
左のおもりが\(M\)、右のおもりが\(m\)。
ひもの長さは\(l=x+y\)。
初期条件は\(x_{0}=a\)、\(\dot x(0)=0\)。
このとき、\(x(t) , y(t)\)を求めよ。
解答
\(C=x+y-l=0\) \(\cdots\) 拘束条件
\(L=\displaystyle\frac{1}{2}M\dot x^2+\displaystyle\frac{1}{2}m\dot y^2+Mgx+mgy\) \(\cdots\) ラグランジアン
未定乗数の方程式は
\(\displaystyle\frac{\partial L}{\partial x}-\displaystyle\frac{d}{dt}\displaystyle\frac{\partial L}{\partial \dot x}+\lambda\displaystyle\frac{\partial C}{\partial x}=0\)より \(Mg-M\ddot x+\lambda=0\)
\(\displaystyle\frac{\partial L}{\partial y}-\displaystyle\frac{d}{dt}\displaystyle\frac{\partial L}{\partial \dot y}+\lambda\displaystyle\frac{\partial C}{\partial y}=0\)より \(mg-m\ddot y+\lambda=0\)
\(\lambda\)を引き算によって消去し、\(\ddot x=-\ddot y\)を使って整理すると、\(\ddot x=\displaystyle\frac{M-m}{M+m}g\)
初期条件を考慮すると
$$x(t)=a+\displaystyle\frac{M-m}{2(M+m)}gt^2$$
$$y(t)=l-a-\displaystyle\frac{M-m}{2(M+m)}gt^2$$

