[mathjax]
目次
問題
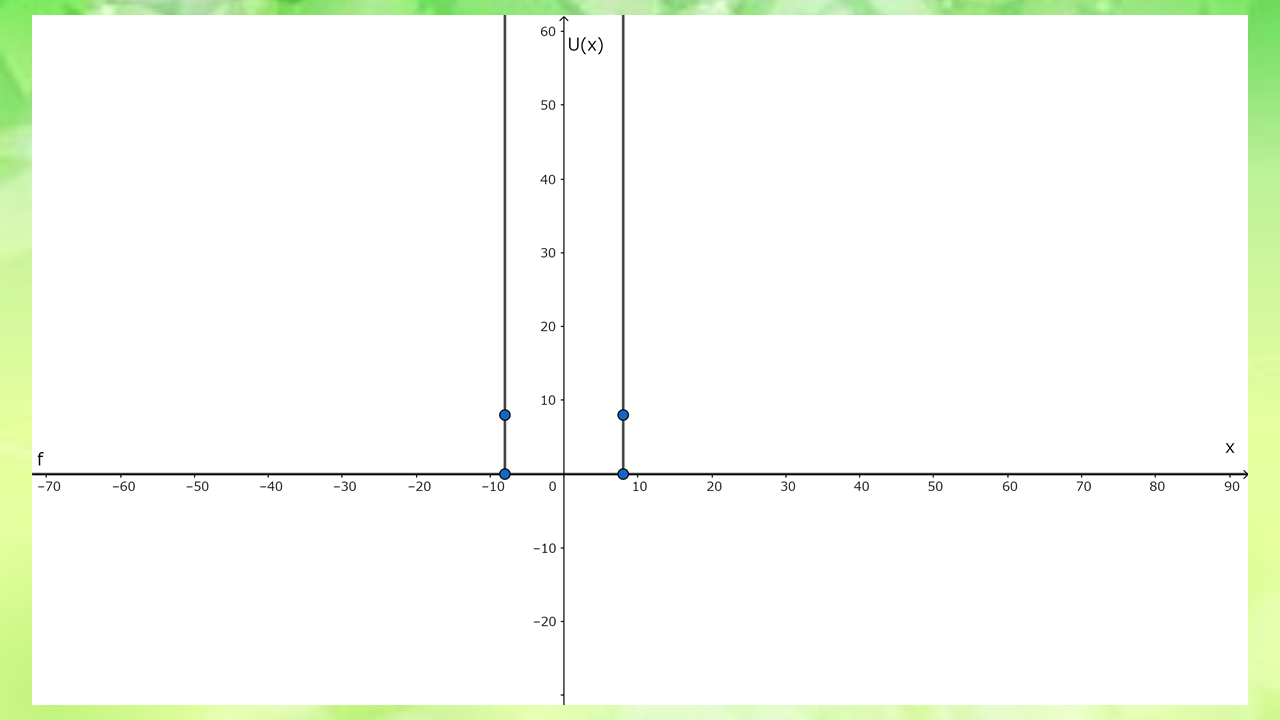
\(E<U_{0}\)の束縛状態を考える。
$$\begin{cases}U(x)=0 & |x|\leq a \\ U(x)=U_{0} & |x|\geq a \end{cases}$$
というときにシュレディンガー方程式を解く。
解答
一次元のシュレディンガー方程式は\(\biggl[-\displaystyle\frac{\hbar^2}{2m}\displaystyle\frac{\partial^2}{\partial x^2}+U(x)\biggr]\psi(x)=E\psi(x)\)
\(|x|< a\)
\(U(x)=0\)をシュレディンガー方程式に代入すると
$$-\displaystyle\frac{\hbar^2}{2m}\displaystyle\frac{\partial^2 \psi(x)}{\partial x^2}=E\psi(x)$$
$$\displaystyle\frac{\partial^2 \psi(x)}{\partial x^2}=-\displaystyle\frac{2mE}{\hbar^2}\psi(x)$$
\(\psi(x)=A\sin kx+B\cos kx\) \(\left(k=\displaystyle\frac{\sqrt{2mE}}{\hbar}\right)\)
※係数は接続条件、規格化条件から決める。
\(|x|> a\)
\(U(x)=U_{0}\)をシュレディンガー方程式に代入すると
$$-\displaystyle\frac{\hbar^2}{2m}\displaystyle\frac{\partial^2 \psi(x)}{\partial x^2}+U_{0}\psi(x)=E\psi(x)$$
$$\displaystyle\frac{\partial^2 \psi(x)}{\partial x^2}=\displaystyle\frac{2m(U_{0}-E)}{\hbar^2}\psi(x)$$
\(\psi(x)=Ce^{\alpha x}+De^{-\alpha x}\) \(\left(\alpha=\displaystyle\frac{\sqrt{2m(U_{0}-E)}}{\hbar}\right)\)
※係数は接続条件、規格化条件から決める。
\(\psi(x)\)の偶関数、奇関数
\(\psi(x)\)は偶関数か奇関数しかありえない。
\(\biggl[-\displaystyle\frac{\hbar^2}{2m}\displaystyle\frac{\partial^2}{\partial x^2}+U(x)\biggr]\psi(x)=E\psi(x)\)
\(x\) を \(-x\) にすると\(U(x)\)が偶関数なので
\(\biggl[-\displaystyle\frac{\hbar^2}{2m}\displaystyle\frac{\partial^2}{\partial x^2}+U(x)\biggr]\psi(-x)=E\psi(-x)\)
固有値が同じなので固有ベクトルは定数倍だけ違う。
\(\psi(x)=a\psi(-x)\)
\(\psi(-x)=a\psi(x)\) (逆も成り立つため)
\(a=\pm 1\) が成り立つので、\(\psi(x)\)は偶関数または奇関数。
解が偶関数の時
\(\psi(x)=Ee^{\alpha x}\) \(x<-a\)
\(\psi(x)=B\cos kx\) \(|x|<a\)
\(\psi(x)=Ee^{-\alpha x}\) \(x>a\)
境界条件
\(B\cos ka=E e^{-\alpha a}\) \(\cdots\) ①
\(-kB\sin ka=-\alpha E e^{-\alpha a}\) \(\cdots\) ②
ここから \(\alpha=k\tan ka \cdots \) ③の関係が導ける。
規格化条件
\(\displaystyle\int_{-\infty}^{\infty} \psi(x)^2 dx=1\) を課す。偶関数なので
\(1=2\displaystyle\int_{0}^{a} (B\cos kx)^2 dx+2\displaystyle\int_{a}^{\infty} (Ee^{-\alpha x})^2 dx\)
\(=B^2\biggl(a+\displaystyle\frac{\sin 2ka}{2k}\biggr)+\displaystyle\frac{E^2 e^{-2\alpha a}}{\alpha}\)
\(=B^2\biggl(a+\displaystyle\frac{\sin^2 ka}{k\tan ka}+\displaystyle\frac{\cos^2 ka}{\alpha}\biggr)\) ①を使った。
\(=B^2\biggl(a+\displaystyle\frac{1}{\alpha}\biggr)\) ③を使った。
よって \(B=\displaystyle\frac{1}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
①に代入すると \(E=\displaystyle\frac{e^{\alpha a}\cos ka}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
結果
\(x<-a\)のとき \(\psi(x)=\displaystyle\frac{e^{\alpha (x+a)}\cos ka}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
\(|x|<a\)のとき \(\psi(x)=\displaystyle\frac{\cos kx}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
\(x>a\)のとき \(\psi(x)=\displaystyle\frac{e^{-\alpha (x-a)}\cos ka}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
\(E\)は具体的には求まらないが、\(\alpha=k\tan ka \cdots \)と\(k^2+\alpha^2=\displaystyle\frac{2m(U_{0}-E)}{\hbar} \)の交点から解の個数などは調べられる。
解が奇関数の時
\(\psi(x)=Ee^{\alpha x}\) \(x<-a\)
\(\psi(x)=A\sin kx\) \(|x|<a\)
\(\psi(x)=-Ee^{-\alpha x}\) \(x>a\)
境界条件
\(A\sin ka=-E e^{-\alpha a}\) \(\cdots\) ④
\(kA\cos ka=\alpha E e^{-\alpha a}\) \(\cdots\) ⑤
ここから \(\alpha=-k\cot ka \cdots \) ⑥の関係が導ける。
規格化条件
\(\displaystyle\int_{-\infty}^{\infty} \psi(x)^2 dx=1\) を課す。奇関数の二乗は偶関数なので同様にできて
\(1=2\displaystyle\int_{0}^{a} (A\sin kx)^2 dx+2\displaystyle\int_{a}^{\infty} (-Ee^{-\alpha x})^2 dx\)
\(=A^2\biggl(a-\displaystyle\frac{\sin 2ka}{2k}\biggr)+\displaystyle\frac{E^2 e^{-2\alpha a}}{\alpha}\)
\(=A^2\biggl(a-\displaystyle\frac{\cos^2 ka\tan ka}{k}+\displaystyle\frac{\sin^2 ka}{\alpha}\biggr)\) ④を使った。
\(=A^2\biggl(a+\displaystyle\frac{1}{\alpha}\biggr)\) ⑥を使った。
よって \(A=\displaystyle\frac{1}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
①に代入すると \(E=-\displaystyle\frac{e^{\alpha a}\sin ka}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
結果
\(x<-a\)のとき \(\psi(x)=-\displaystyle\frac{e^{\alpha (x+a)}\sin ka}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
\(|x|<a\)のとき \(\psi(x)=\displaystyle\frac{\sin kx}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
\(x>a\)のとき \(\psi(x)=\displaystyle\frac{e^{-\alpha (x-a)}\sin ka}{\sqrt{a+\displaystyle\frac{1}{\alpha}}}\)
\(E\)は具体的には求まらないが、\(\alpha=-k\cot ka \cdots \)と\(k^2+\alpha^2=\displaystyle\frac{2m(U_{0}-E)}{\hbar} \)の交点から解の個数などは調べられる。