目次
問題
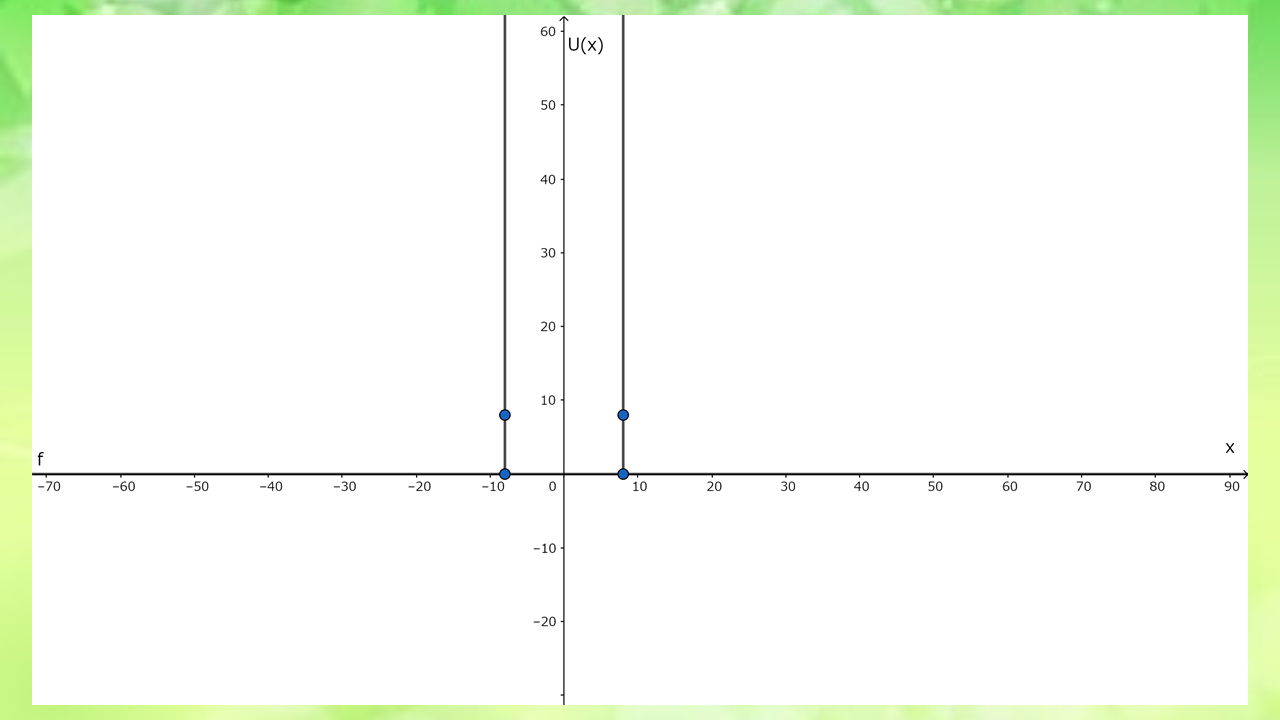
$$\begin{cases} U(x)=0 & |x|\leq a \\ U(x)=\infty & |x|\geq a \end{cases}$$
というときにシュレディンガー方程式を解く。
解答
一次元のシュレディンガー方程式は\(\biggl[-\displaystyle\frac{\hbar^2}{2m}\displaystyle\frac{\partial^2}{\partial x^2}+U(x)\biggr]\psi(x)=E\psi(x)\)
\(|x|> a\)
\(|x|\geq a\)では \(U(x)=\infty\) なので式を満たすには \(\psi(x)=0\)にならざるを得ない。(ポテンシャルが無限大で入れず、存在確率$0$)
\(|x|< a\)
\(U(x)=0\)をシュレディンガー方程式に代入すると
$$-\displaystyle\frac{\hbar^2}{2m}\displaystyle\frac{\partial^2 \psi(x)}{\partial x^2}=E\psi(x)$$
$$\displaystyle\frac{\partial^2 \psi(x)}{\partial x^2}=-\displaystyle\frac{2mE}{\hbar^2}\psi(x)$$
\(\psi(x)=A\sin kx+B\cos kx\) \(\left(k=\displaystyle\frac{\sqrt{2mE}}{\hbar}\right)\)
※係数は接続条件、規格化条件から決める。
境界条件
\(\psi(a)=0\) 及び \(\psi(-a)=0\)
\(A\sin ka+B\cos ka=0\) かつ\(-A\sin ka+B\cos ka=0\)
これを満たすには、\(A\sin ka=0\) かつ \(B\cos ka=0\) である。
解の候補
① \(A=B=0\) …… 意味をなさない。
② \(A=0\)、\(\cos ka=0\) …… 解
③ \(B=0\)、\(\sin ka=0\) …… 解
④ \(\cos ka=0\)、\(\sin ka=0\) …… 存在しない
②のとき
\(ka=\biggl(n+\displaystyle\frac{1}{2}\biggr)\pi\) である。 \(\psi(x)=A\sin kx+B\cos kx\) に代入して
\(\psi(x)=B\cos \displaystyle\frac{(2n+1)\pi}{2a} x\)
\(E=\displaystyle\frac{\hbar^2 k^2}{2m}=\displaystyle\frac{\hbar^2 \pi^2}{8ma^2}(2n+1)^2\)
・エネルギーはとびとびの値を取っていて、最低状態でも0にならない。
③のとき
\(ka=n\pi\) である。\(\psi(x)=A\sin kx+B\cos kx\) に代入して
\(\psi(x)=A\sin \displaystyle\frac{2n\pi}{2a} x\)
\(E=\displaystyle\frac{\hbar^2 k^2}{2m}=\displaystyle\frac{\hbar^2 \pi^2}{8ma^2}(2n)^2\)
規格化条件
\(\displaystyle\int_{-\infty}^{\infty} \psi(x)^2 dx=1\) を課すと
\(1=\displaystyle\int_{-a}^{a} \left(B\cos \displaystyle\frac{(2n+1)\pi}{2a} x\right)^2 dx=\displaystyle\int_{-a}^{a} \left(A\sin \displaystyle\frac{2n\pi}{2a} x \right)^2 dx\)
\(A=B=\displaystyle\frac{1}{\sqrt{a}}\)
結果
\(|x|\leqq a\)のとき
\(\psi(x)=\displaystyle\frac{1}{\sqrt{a}}\cos\displaystyle\frac{n\pi x}{2a}\) \(n\)は奇数。
\(\psi(x)=\displaystyle\frac{1}{\sqrt{a}}\sin\displaystyle\frac{n\pi x}{2a}\) \(n\)は偶数。
\(|x|\geqq a\)のとき
\(\psi(x)=0\)