[mathjax]
鏡像法(電気映像法)の問題です。
目次
問題
原点中心半径\(a\)の導体球があり、その外部\((d,0,0)\)に電荷\(q\)がある。このとき
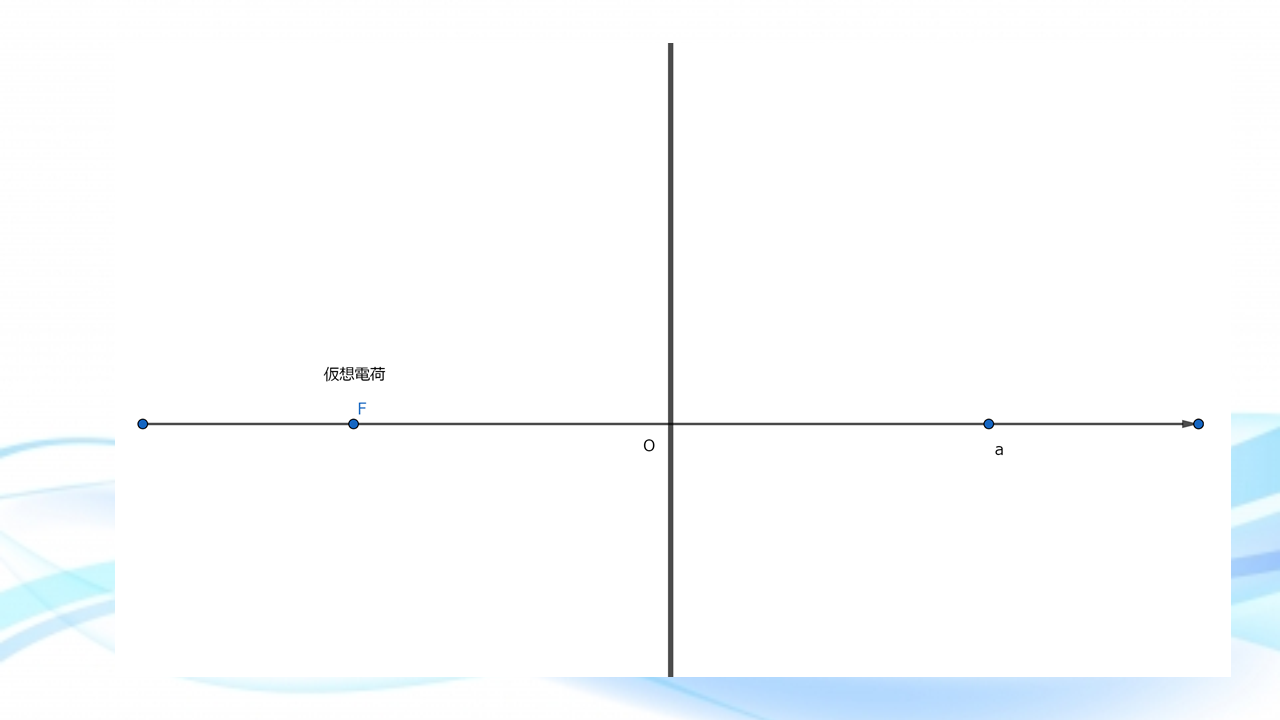
① 仮想電荷の位置と電荷量は?
② 表面電荷密度は?
③ 球上に現れる総電荷は?
解答
1番
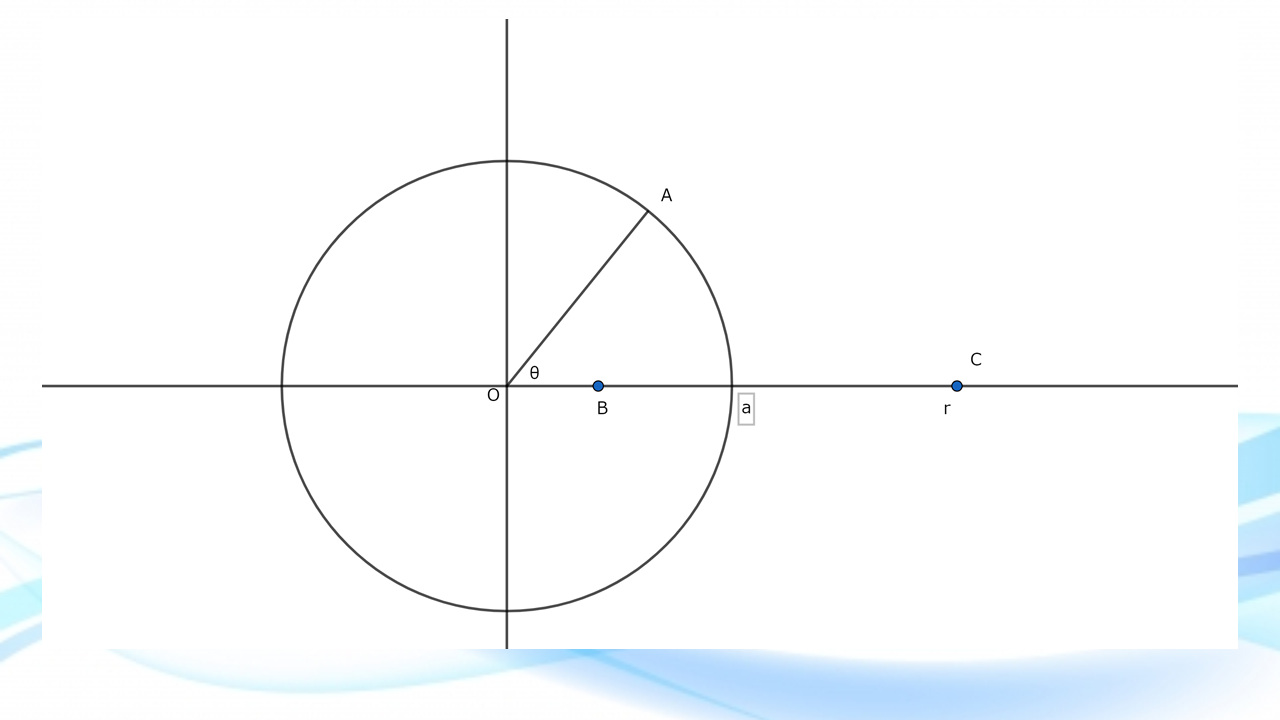
\((l,0,0)\)に\(q^{\prime}\)があると仮定する。
余弦定理より
\(AC^2=a^2+d^2-2ad\cos\theta\)
\(AB^2=a^2+l^2-2al\cos\theta\)
\(\phi=\displaystyle\frac{1}{4\pi\epsilon_{0}} \biggl(\displaystyle\frac{q}{AC}+\displaystyle\frac{q^{\prime}}{AB}\biggr)\)
導体平面上で\(\phi=0\)となることより
\(\displaystyle\frac{q}{AC}+\displaystyle\frac{q^{\prime}}{AB}=0\)
変形すると \(q^2 AB^2={q^{\prime}}^2 AC^2\)
余弦定理の式を代入すると
\(q^2 (a^2+l^2-2al\cos\theta)={q^{\prime}}^2 (a^2+d^2-2ad\cos\theta)\)
\(q^2 (a^2+l^2)-{q^{\prime}}^2 (a^2+d^2)+(2ad{q^{\prime}}^2-2alq^2)\cos\theta=0\)
これが\(\theta\)によらないので
\(q^2 (a^2+l^2)={q^{\prime}}^2 (a^2+d^2)\)、\(-2al q^2=-2ad {q^{\prime}}^2\)
後ろの式から \(\displaystyle\frac{{q^{\prime}}^2}{q^2}=\displaystyle\frac{l}{d}\)
前の式に代入して計算すると
\((d-l)(a^2-dl)=0\)
\(d\neq l\)より \(l=\displaystyle\frac{a^2}{d}\) である。
このとき
\({q^{\prime}}^2=\displaystyle\frac{l}{d}q^2=\displaystyle\frac{a^2 q^2}{d^2}\)
\(q^{\prime}<0\)より \(q^{\prime}=-\displaystyle\frac{aq}{d}\)
2番
ポテンシャル\(\phi\)は
\(\phi=\displaystyle\frac{1}{4\pi \epsilon_{0}}\biggl(\displaystyle\frac{q}{\sqrt{r^2+d^2-2rd\cos\theta}}+\displaystyle\frac{-\displaystyle\frac{aq}{d}}{\sqrt{r^2+\biggl(\displaystyle\frac{a^2}{d}\biggr)^2-2r\displaystyle\frac{a^2}{d}\cos\theta}}\biggr)\)
であり、表面電荷密度は
\(\omega=-\epsilon_{0}\displaystyle\frac{\partial \phi}{\partial r}\biggr|_{r=a}\)
\(=-\displaystyle\frac{q}{4\pi}\biggl[-\displaystyle\frac{1}{2}\cdot\displaystyle\frac{2a-2d\cos\theta}{(a^2+d^2-2ad\cos\theta)^{\frac{3}{2}}}+\displaystyle\frac{a}{2d}\cdot\displaystyle\frac{2a-2\displaystyle\frac{a^2}{d}\cos\theta}{(a^2+\displaystyle\frac{a^4}{d^2}-2\displaystyle\frac{a^3}{d}\cos\theta)^{\frac{3}{2}}}\biggr]\)
\(=\displaystyle\frac{q}{4\pi}\biggl[\displaystyle\frac{1}{2}\cdot\displaystyle\frac{a-d\cos\theta}{(a^2+d^2-2ad\cos\theta)^{\frac{3}{2}}}-\displaystyle\frac{a^2}{d^2}\cdot\displaystyle\frac{d-a\cos\theta}{\displaystyle\frac{a^3}{d^3}(a^2+d^2-2ad\cos\theta)^{\frac{3}{2}}}\biggr]\)
\(=\displaystyle\frac{q}{4\pi}\biggl[\displaystyle\frac{1}{2}\cdot\displaystyle\frac{a-d\cos\theta}{(a^2+d^2-2ad\cos\theta)^{\frac{3}{2}}}-\displaystyle\frac{\displaystyle\frac{d^2}{a}-d\cos\theta}{\displaystyle\frac{a^3}{d^3}(a^2+d^2-2ad\cos\theta)^{\frac{3}{2}}}\biggr]\)
\(=\displaystyle\frac{q}{4\pi a}\displaystyle\frac{a^2-d^2}{(a^2+d^2-2ad\cos\theta)^{\frac{3}{2}}}\)
3番
2番の結果を導体表面全体にわたって積分する。
\(Q=\displaystyle\int_{0}^{2\pi}\displaystyle\int_{0}^{\pi}\displaystyle\frac{q}{4\pi a}\displaystyle\frac{a^2-d^2}{(a^2+d^2-2ad\cos\theta)^{\frac{3}{2}}} a^2\sin\theta d\theta d\phi\)
\(=\displaystyle\frac{qa}{4\pi}(a^2-d^2)\displaystyle\int_{0}^{2\pi}d\phi \displaystyle\int_{0}^{\pi}\displaystyle\frac{\sin\theta}{(a^2+d^2-2ad\cos\theta)^{\frac{3}{2}}} d\theta\)
\(=\displaystyle\frac{qa}{2}(a^2-d^2)\displaystyle\int_{1}^{-1}\displaystyle\frac{-dt}{(a^2+d^2-2adt)^{\frac{3}{2}}}\) \(\cdots\) \(t=\cos\theta\)
\(=\displaystyle\frac{qa}{2}(a^2-d^2) \biggl[\displaystyle\frac{1}{ad}(a^2+d^2-2adt)^{-\frac{1}{2}}\biggr]_{-1}^{1}\)
\(=\displaystyle\frac{q}{2d}(a^2-d^2)\biggl(\displaystyle\frac{1}{d-a}-\displaystyle\frac{1}{d+a}\biggr)\)
\(=-\displaystyle\frac{a}{d}q\)