目次
トンネル効果
古典的には存在が許されないポテンシャル障壁を超えた領域に、量子力学的には粒子が存在しうるという効果のことをトンネル効果という。粒子があたかもトンネルをすり抜けたかのように移動する。
計算
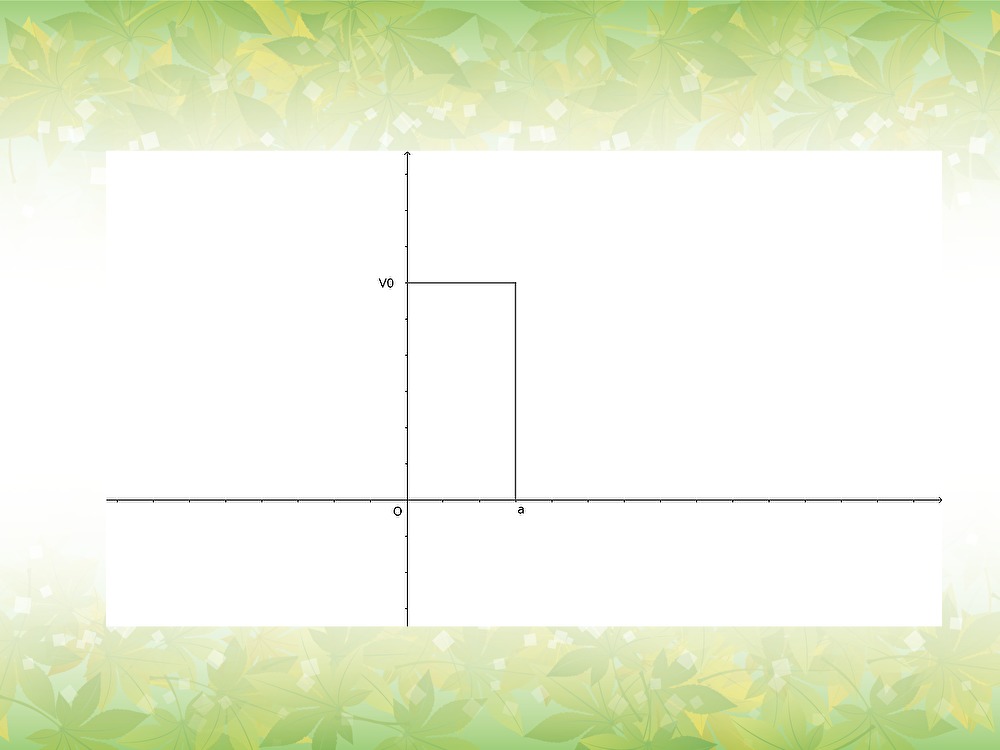
以下のような状況を考える。
\(V(x)=\begin{cases} 0 & x\leq 0 \\ \\ V_{0} & 0\leq x\leq a \\ \\ 0 & x\geq a \end{cases}\)
\(E>V_{0}\)のとき
各領域での波動関数
シュレディンガー方程式は \(\biggl[-\displaystyle\frac{\hbar^2}{2m}\displaystyle\frac{d^2}{dx^2}+V(x)\biggr]\psi(x)=E\psi(x)\)
\(x\leq 0\)のとき
\(V(x)=0\)なので \(\displaystyle\frac{d^2 \psi}{dx^2}=-\displaystyle\frac{2mE}{\hbar^2}\psi\)
これを解くと
\(\psi=Ae^{ikx}+Be^{-ikx}\) ※\(k=\displaystyle\frac{\sqrt{2mE}}{\hbar}\)
\(0\leq x\leq a\)のとき
\(V(x)=V_{0}\)なので
\(\psi=Fe^{i\alpha x}+Ge^{-i\alpha x}\) ※\(\alpha=\displaystyle\frac{\sqrt{2m(E-V_{0})}}{\hbar}\)
\(a\leq x\)のとき
\(V(x)=0\)なので
\(\psi=Ce^{ikx}\) ※\(k=\displaystyle\frac{\sqrt{2mE}}{\hbar}\)
接続条件
ここで\(x=0,a\)での接続条件を課す。(波動関数とその一階微分が連続)
・\(x=0\)での条件
\(A+B=F+G\)
\(ik(A-B)=i\alpha(F-G)\)
・\(x=a\)での条件
\(Fe^{i\alpha a}+Ge^{-i\alpha a}=Ce^{ika}\)
\(i\alpha(Fe^{i\alpha a}-Ge^{-i\alpha a})=ikCe^{ika}\)
結果
これを解くと($F,G$を消す)
$$\displaystyle\frac{B}{A}=\displaystyle\frac{(k^2-\alpha^2)(1-e^{2i\alpha a})}{(\alpha+k)^2-(k-\alpha)^2e^{2i\alpha a}}$$
$$\displaystyle\frac{C}{A}=\displaystyle\frac{4k\alpha e^{i(\alpha-k)a}}{(\alpha+k)^2-(k-\alpha)^2e^{2i\alpha a}}$$
よって反射率\(R\)は
$$R=\biggl|\displaystyle\frac{B}{A}\biggr|^2=\biggl[1+\displaystyle\frac{4k^2\alpha^2}{(k^2-\alpha^2)^2 \sin^2 \alpha a}\biggr]^{-1}$$
透過率\(T\)は
$$T=\biggl|\displaystyle\frac{C}{A}\biggr|^2=\biggl[1+\displaystyle\frac{(k^2-\alpha^2)^2 \sin^2 \alpha a}{4k^2\alpha^2}\biggr]^{-1}$$
※\(R+T=1\)となっている。
※\(\sin \alpha a=0\)のとき\(R=0\)、\(T=1\)となり完全透過。
※完全透過以外の時、\(E>V_{0}\)なのに跳ね返る粒子がある。
\(0<E<V_{0}\)のとき
波動関数は以下のようになる。
$\begin{cases}\psi=Ae^{ikx}+Be^{-ikx} & x\leq 0 \\ \psi=Fe^{-\beta x}+Ge^{\beta x} & 0\leq x\leq a \\ \psi=Ce^{ikx} & x\geq a \end{cases}$
よって、\(E>V_{0}\)の場合の\(\alpha\)を\(i\beta\)とおきかえたもの。
よって反射率\(R\)は
$$R=\biggl|\displaystyle\frac{B}{A}\biggr|^2=\biggl[1+\displaystyle\frac{4k^2\beta^2}{(k^2+\beta^2)^2 \sinh^2 \beta a}\biggr]^{-1}$$
透過率\(T\)は
$$T=\biggl|\displaystyle\frac{C}{A}\biggr|^2=\biggl[1+\displaystyle\frac{(k^2+\beta^2)^2 \sinh^2 \beta a}{4k^2\beta^2}\biggr]^{-1}$$
エネルギーが\(0\leq E\leq V_{0}\)にもかかわらず、透過している(トンネル効果)。