[mathjax]
目次
カージオイド 体積
カージオイドの媒介変数表示を書いておきます。
\(x=r\cos\theta=a\cos\theta(1+\cos\theta)\)
\(y=r\sin\theta=a\sin\theta(1+\cos\theta)\)
以下の計算で使用するので、書いておきます。
\(\displaystyle\frac{dx}{d\theta}=-a\sin\theta(1+2\cos\theta)\)
\(\displaystyle\frac{dy}{d\theta}=a(2\cos^2\theta+\cos\theta-1)\)
カージオイドの記事はこちら(長くなったので分割しました)

\(x\)軸まわり
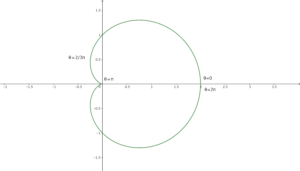
\(0\leq\theta\leq\displaystyle\frac{2\pi}{3}\)の部分の曲線が作る体積から、\(\displaystyle\frac{2\pi}{3}\leq \theta\leq \pi\)までの部分の曲線が作る体積を引くと考える。
※\(x\)軸との交点は、\(y=a\sin\theta(1+\cos\theta)=0\)から出せる。
※\(x\)座標が最小となる点は、\(\displaystyle\frac{dx}{d\theta}=-a\sin\theta(1+2\cos\theta)=0\)から求められる。
すると体積は
\(V=\displaystyle\int_{-\frac{a}{4}}^{2a} \pi y^2 dx-\displaystyle\int_{-\frac{a}{4}}^{0} \pi y^2 dx\)
※\(x\)について積分しているので、積分範囲は\(\theta\)ではなく\(x\)に変換している。(\(\theta\)を媒介変数の\(x\)の式に代入すれば出てきます。)
\(=\displaystyle\int_{0}^{2a} \pi y^2 dx\)
\(=\displaystyle\int_{\pi}^{0} \pi a^2(1+\cos\theta)^2\sin^2\theta\times-\sin\theta(1+2\cos\theta)d\theta\)
※\(y\)や\(dx\)を代入した。
\(=\pi a^3\displaystyle\int_{0}^{\pi} \sin^3\theta(1+2\cos\theta)(1+\cos\theta)^2 d\theta\)
ここで\(t=\cos\theta\)とすると
\(=\pi a^3\displaystyle\int_{1}^{-1} -(1-t^2)(1+2t)(1+t)^2 dt\)
\(=\pi a^3\displaystyle\int_{-1}^{1} (-2t^5-5t^4-2t^3+4t^2+4t+1)dt\)
\(=2\pi a^3\biggl[-t^5+\displaystyle\frac{4}{3}t^3+t\biggr]_{0}^{1}\)
※偶関数と奇関数の性質を利用しましたが、分かりにくければ、そのままやっても大丈夫です。
\(=\displaystyle\frac{8}{3}\pi a^3\)
\(y\)軸まわり

上半分を二倍すると考える。\(x<0\)の部分は折り返すと重なるので考えなくてよい。
\(0\leq\theta\leq\displaystyle\frac{\pi}{3}\)の部分の曲線が作る体積から、\(\displaystyle\frac{\pi}{3}\leq\theta\leq \displaystyle\frac{\pi}{2}\)までの部分の曲線が作る体積を引くと考える。
※\(y\)軸との交点は、\(x=a\cos\theta(1+\cos\theta)=0\)から出せる。
※\(y\)座標が最大となる点は、\(\displaystyle\frac{dy}{d\theta}=-a(2\cos^2\theta+\cos\theta-1)=0\)から求められる。
すると体積は
\(V=2\displaystyle\int_{0}^{\frac{3\sqrt{3}}{4}a} x^2 dy-2\displaystyle\int_{a}^{\frac{3\sqrt{3}}{4}a} x^2 dy\)
※\(y\)について積分しているので、積分範囲は\(\theta\)ではなく\(y\)に変換している。(\(\theta\)を媒介変数の\(y\)の式に代入すれば出てきます。)
\(=2\displaystyle\int_{0}^{a} x^2 dy\)
\(=2\displaystyle\int_{0}^{\frac{\pi}{2}} a^2(1+\cos^2\theta)^2\cos^2\theta\times a(2\cos^2\theta+\cos\theta-1)d\theta\)
※\(x\)や\(dy\)を代入した。
\(=2a^3\displaystyle\int_{0}^{\frac{\pi}{2}} (2\cos^6\theta+5\cos^5\theta+3\cos^4\theta-\cos^3\theta-\cos^2\theta)d\theta\)
\(=2a^3\displaystyle\int_{0}^{\frac{\pi}{2}} (2\cos^6\theta+3\cos^4\theta-\cos^2\theta)d\theta+2a^3\displaystyle\int_{0}^{\frac{\pi}{2}} (5\cos^5\theta-\cos^3\theta)d\theta\)
ここで https://kikyousan.com/mathbottop/integralbot/integralbot40 の結果を利用する。
対称なので、\(\sin\theta\)でも\(\cos\theta\)でも同じ結果になります。
\(=2a^3\biggl(2\cdot \displaystyle\frac{5\cdot 3\cdot 1}{6\cdot 4\cdot 2}+3\cdot\displaystyle\frac{3\cdot 1}{4\cdot 2}-\displaystyle\frac{1}{2}\biggr)\displaystyle\frac{\pi}{2}+2a^3\biggl(5\cdot \displaystyle\frac{4\cdot 2}{5\cdot 3\cdot 1}-\displaystyle\frac{2}{3\cdot 1}\biggr)\)
\(=\displaystyle\frac{5}{4}\pi a^3+4a^3\)
結果
\(x\)軸まわりが\(\displaystyle\frac{8}{3}\pi a^3\)
\(y\)軸まわりが\(\displaystyle\frac{5}{4}\pi a^3+4a^3\)
