目次
対数正規分布
対数正規分布は次のような確率密度関数をもちます。
$f(x) = \displaystyle\frac{1}{\sqrt{2\pi\sigma^2}x}\exp\left(-\displaystyle\frac{(\log x – \mu)^2}{2\sigma^2}\right) \quad (x>0)$
この分布に従う確率変数の対数をとると正規分布に従うことが名前の由来となっています。
資産の分布がこれに従うといわれています。
$f(y)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}} \mathrm{exp}\left(-\displaystyle\frac{(y-\mu)^2}{2\sigma^2}\right)$
$Y=\log X$と変換すると
$g(x)=f(y)\displaystyle\frac{dy}{dx}=f(\log x)\displaystyle\frac{1}{x}=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}x}\exp\left(-\displaystyle\frac{(\log x – \mu)^2}{2\sigma^2}\right)$
期待値
$E[X^k]=\displaystyle\int_{0}^{\infty} x^k\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}x}\exp\left(-\displaystyle\frac{(\log x – \mu)^2}{2\sigma^2}\right)$
$t=\log x$と変換すると
$=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}\displaystyle\int_{-\infty}^{\infty} \mathrm{exp}\left[-\frac{1}{2\sigma^2} [(t-(\mu+\sigma^2 k))^2-2\mu\sigma^2 k-\sigma^4 k^2]\right] dt$
$=e^{\mu k+\frac{\sigma^2 k^2}{2}}$
期待値は$k=1$として、$E[X]=e^{\mu+\frac{\sigma^2 }{2}}$となります。
分散
$k=2$とすると$E[X]=e^{2\mu+2\sigma^2}$となるので
$V[X]=E[X^2]-E[X]^2=e^{2\mu+\sigma^2}(e^{\sigma^2}-1)$
累積分布関数
$F(X)=\displaystyle\frac{1}{2}\left(1+\mathrm{erf}\left(\displaystyle\frac{\log x-\mu}{\sigma\sqrt{2}}\right)\right)$
※$erf(x)$は誤差関数です
グラフ

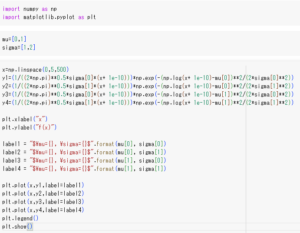
code
[1e-10]は、0で割らないための微小量で本質的な意味はないです。