[mathjax]
目次
Euler-Lagrange方程式
$$\displaystyle\frac{\partial L}{\partial x_{i}}-\displaystyle\frac{d}{dt}\displaystyle\frac{\partial L}{\partial \dot x_{i}}=0$$
1番 運動方程式
保存力下での一質点の物体を考える。ラグランジアンは
$$L=\displaystyle\frac{1}{2}m\dot x_{i}^2-U(x_{i})$$
Euler-Lagrange方程式を変形していく。
\(\displaystyle\frac{\partial L}{\partial x_{i}}-\displaystyle\frac{d}{dt}\displaystyle\frac{\partial L}{\partial \dot x_{i}}=0\)
\(\Leftrightarrow\) \(-\nabla U-\displaystyle\frac{d}{dt}(m\dot x_{i})=0\)
\(\Leftrightarrow\) \(m\ddot x_{i}=-\nabla U\)
\(\Leftrightarrow\) \(m\ddot x=F\) (※保存力なので\(F=-\nabla U\))
2番 単振り子
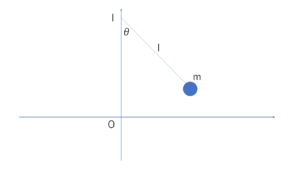
上のような単振り子を考える。条件を整理する。
おもり座標 \((x , y)=(l\sin\theta , l-l\cos\theta)\)
微分すると \((\dot x , \dot y)=(l\dot\theta\cos\theta,l\dot\theta\sin\theta)\)
ラグランジアンは
$$L=U-T=\displaystyle\frac{1}{2}mv^2-mgy=\displaystyle\frac{1}{2}m(\dot x^2+\dot y^2)-mgy$$
$$=\displaystyle\frac{1}{2}ml^2\dot\theta^2-mgl(1-\cos\theta)$$
これをオイラーラグランジュ方程式に代入する。(力学変数は\(\theta\))
\(\displaystyle\frac{\partial L}{\partial\theta}-\displaystyle\frac{d}{dt }\displaystyle\frac{\partial L}{\partial \dot\theta}=0\)
\(\Leftrightarrow\) \(-mgl\sin\theta-\displaystyle\frac{d}{dt}(ml^2\dot\theta)=0\)
\(\Leftrightarrow\) \(-mgl\sin\theta-ml^2\ddot\theta=0\)
\(\Leftrightarrow\) \(\ddot\theta=-\displaystyle\frac{g}{l}\sin\theta\)

